Capítulo 4 Modelos Estatísticos

O objetivo principal da análise de séries temporais é desenvolver modelos matemáticos que ofereçam uma descrição plausível do dado amostral. Nós vamos assumir que uma série temporal pode ser definida como uma coleção de variáveis aleatórias indexadas de acordo com a ordem que elas são obtidas no tempo.

Por exemplo, podemos considerar uma série temporal como uma sequência de variáveis aleatórias \(y_1, y_2, y_3, ...\), onde a variável aleatória \(y_1\) denota o valor tomado de uma série no primeiro período do tempo, a variável \(y_2\) denota o valor para o segundo período no tempo, e assim em diante. Em geral, uma coleção de variáveis aleatórias, \(\{Y_t\}\), indexada por \(t\) é referida como um processo estocástico.

4.1 Ruído Branco

Ruído branco é um tipo muito simples de série gerada como uma coleção de variáveis aleatoriamente não correlacionadas, \(w_t\), com média 0 e variância finita \(\sigma^2_w\). A figura 4.1 mostra uma série desse tipo.

ruido_branco = rnorm(200,0,1)
df = data.frame(ruido_branco = as.matrix(ruido_branco), x = time(ruido_branco)) 


df %>% 
  ggplot(aes(x = x, y = ruido_branco)) +
  geom_line() + 
  labs(x = "Tempo", y = "y",
       title = "Série Temporal do Tipo Ruido Branco")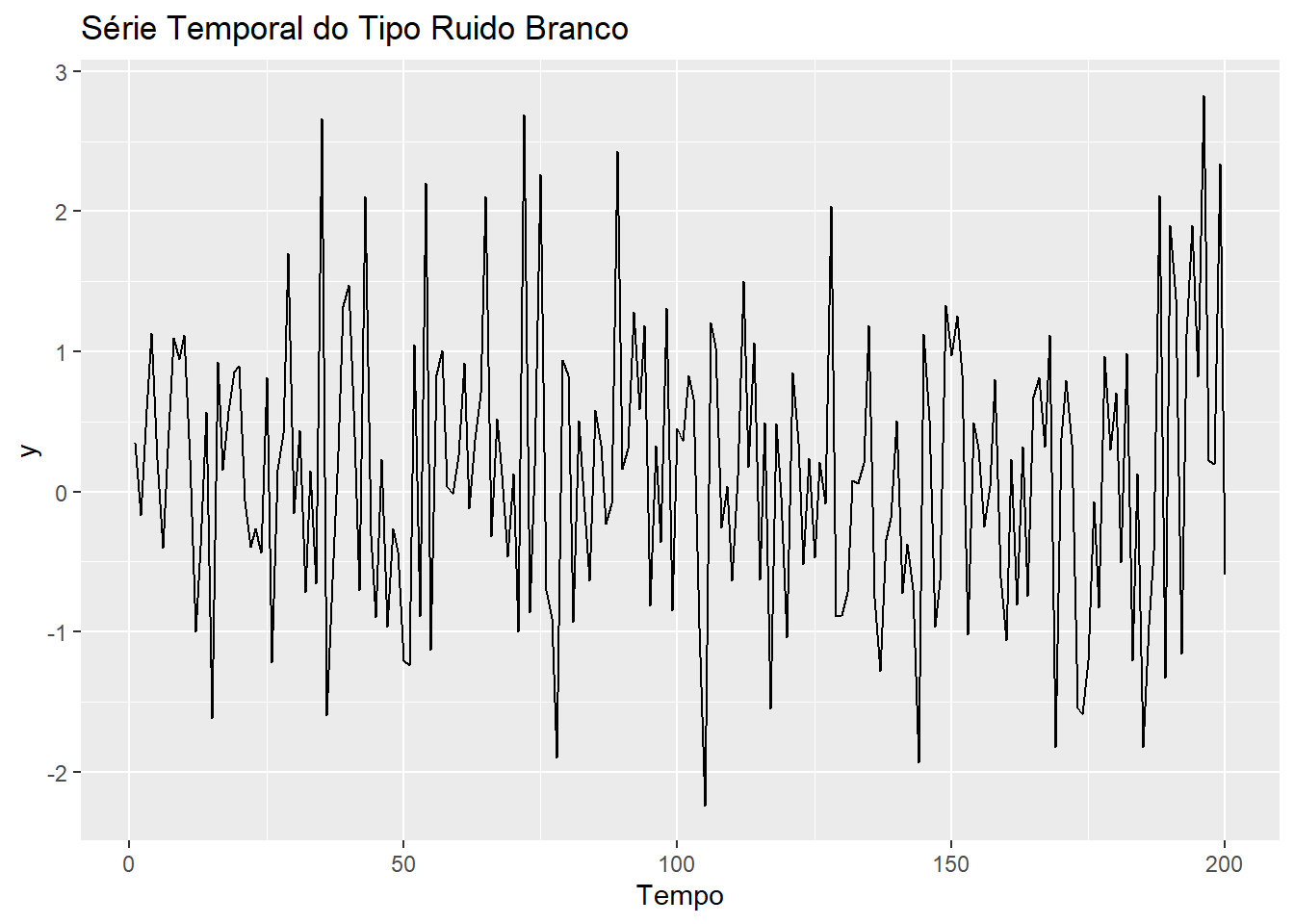

Figure 4.1: Série Temporal do Tipo Ruído Branco

4.2 Média Móvel e Filtro

Podemos substituir a série de ruído branco \(w_t\) por uma média móvel que suaviza a série. Por exemplo, considere substituir \(w_t\) por uma média dos seus valores atuais e dos seus valores vizinhos no passado e no futuro. Assim, deixe que:

\[v_t = \frac{1}{3} (w_{t-1} + w_t + w_{t+1})\]

que faz com que a série tenha a aparência mostrada na figura 4.2.

df <- df %>% 
  mutate(media_movel = stats::filter(ruido_branco, sides = 2, filter = rep(1/3, 3)))

df %>% 
  ggplot(aes(x = x, y = media_movel)) +
  geom_line() + 
  labs(x = "Tempo", y = "y",
       title = "Série Temporal de Média Móvel")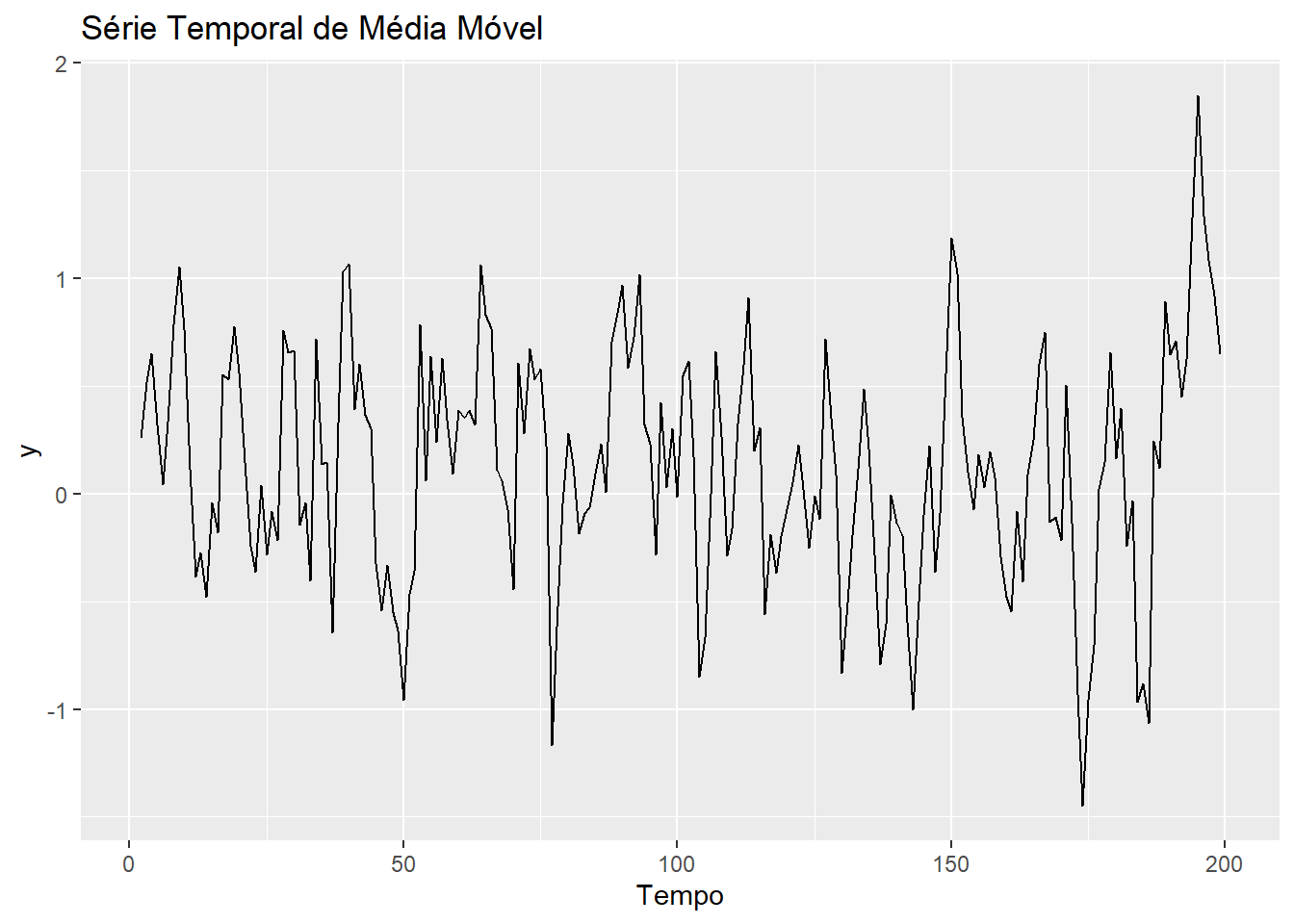

Figure 4.2: Série temporal de Média Móvel

Uma inspeção da série mostra uma versão mais suavizada do gráfico de ruído branco é produzida, refletindo o fato que oscilações grandes são menos aparentes.

4.3 Autoregressões

Suponha que consideremos possamos calcular uma série \(y\) como uma equação de segunda-ordem da série de ruídos brancos \(w_t\):

\[y_t = y_{t-1} - 0.9y_{t-2} + w_t\]

para \(t=1,2,...,500\).

A equação acima representa uma regressão ou previsão dos valores atuais \(x_t\) de uma série temporal como uma função dos dois valores passados da série, e portanto, o termo autoregressivo é sugerido para este modelo.

Temos aqui um problema com os valores iniciais da série uma vez que as condições iniciais são importantes (\(x_0\) e \(x_{-1}\)). Mas, assumindo que temos estes valores, podemos gerar uma sequência de valores apenas substituindo estes valores iniciais na equação acima. O resultado é exibindo na figura 4.3.

ruido_branco <- rnorm(250,0,1)
# as primeiras 50 observações são excluídas para evitar problemas de startup
autoregressivo <- stats::filter(ruido_branco, filter=c(1,-.9), method = "recursive")[-(1:50)]

df <- df %>% 
  mutate(autoregressivo = autoregressivo)

df %>% 
  ggplot(aes(x = x)) +
  geom_line(aes(y = autoregressivo)) + 
  labs(x = "Tempo", y = "y",
       title = "Autogressivo")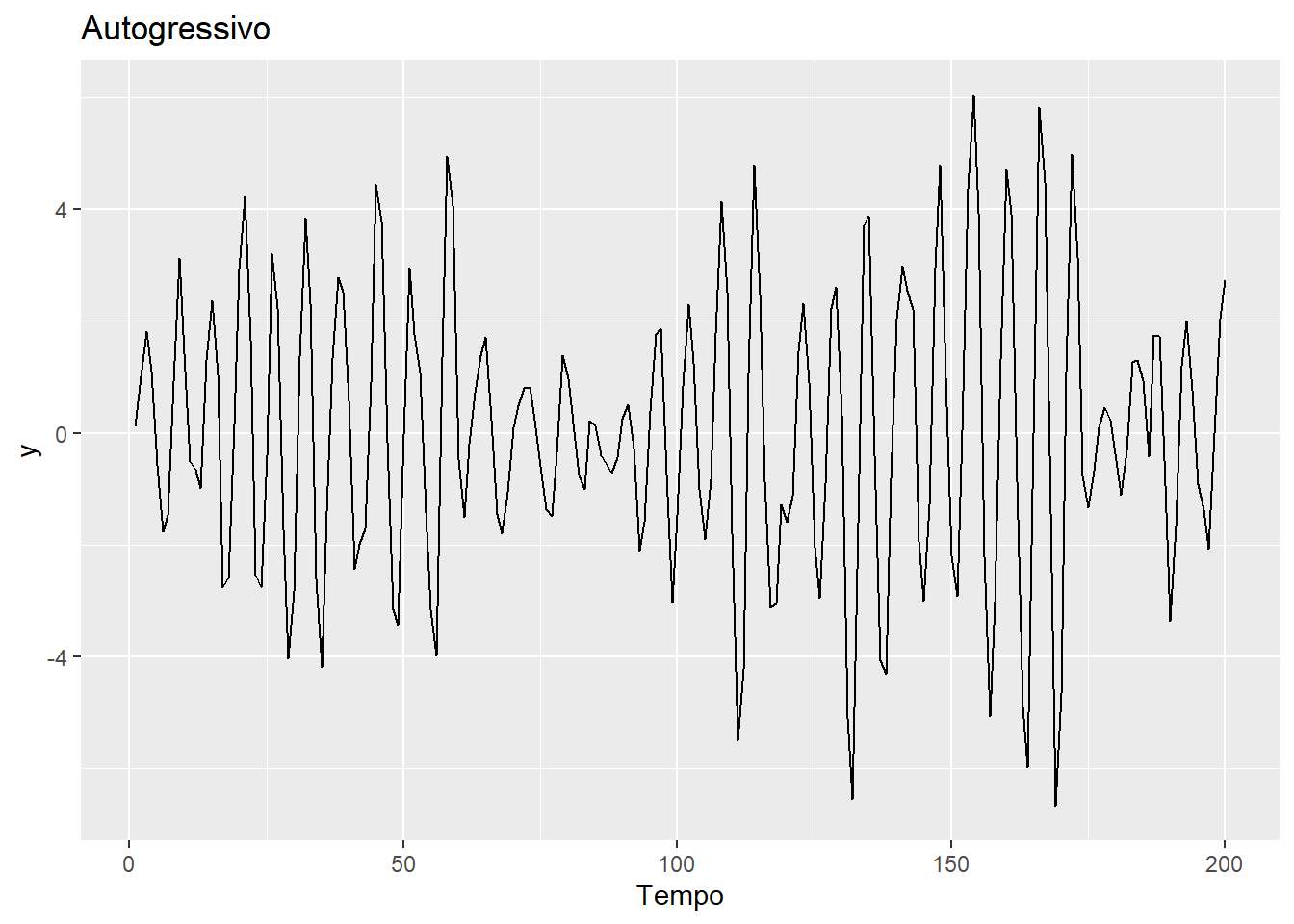

Figure 4.3: Série Temporal Autoregressiva

O modelo autoregressivo acima mostra um comportamento periódico. O modelo autoregressivo acima e suas generalizações podem ser utilizados como um modelo explicativo para muitos tipos de séries observadas.

4.4 Random Walk com Drift

Um modelo para analisar tendências, como as vistas em temperaturas globais, é o random walk com drift. Intuitivamente, em cada período do tempo, a variável toma um passo independente para cima ou para baixo, por isso o termo random walk.

A variável vai subir ou descer? A probabilidade dos dois eventos é igual. Uma analogia comumente utilizada é a de um bêbado caminhando em zig-zag pela rua enquanto tenta se mover em frente: o caminho que ele segue é uma caminhada aleatória ou random walk.

Assim, o modelo de random walk pode ser definido pela equação:

\[y_t = \delta + y_{t-1} + w_t\]

para \(t = 1,2,...,...\) com condições iniciais \(y_0 = 0\) e onde \(w_t\)é um ruido branco. A constante \(\delta\) é chamada de drift, e quando \(\delta = 0\), chamamos o modelo simplesmente de random walk. Quando \(\delta =0\), o valor da série em \(t\) é o valor da variável no tempo \(t-1\) mais um movimento completamente aleatório determinado por \(w_t\). Note que podemos reescrever a equação do random walk com drift ao acumular a soma de vários ruídos brancos:

\[x_t = \delta t + \sum_{j=1}^t w_t\]

para \(t = 1,2,...\). Ou seja, a série é uma soma de passos erráticos. O random walk é um processo que fornece um bom modelo para fenômenos tão diversos quanto preço de ações ou a posição de particulas pequenas suspensas em um flúido (movimento Browniano).

A figura 4.4 mostra 500 observações geradas a partir de um modelo com \(\delta= 0\), \(\delta = 0.2\) e \(\delta_w = 1\).

set.seed(154)

ruido_branco  = rnorm(200)
random_walk = cumsum(ruido_branco)
ruido_branco_drift = ruido_branco + 0.2
random_walk_drift = cumsum(ruido_branco_drift)

df <- df %>% 
  mutate(random_walk = random_walk) %>% 
  mutate(random_walk_drift = random_walk_drift)

df %>% 
  ggplot(aes(x = x)) + 
  geom_line(aes(y = random_walk, color = "Random Walk")) +
  geom_line(aes(y = random_walk_drift, color = "Random Walk com Drift")) +
  labs(x = "Tempo", y = "",
       title = "Random Walk",
       subtitle = "Random Walk sem Drift e Random Walk com Drift",
       color = "Modelo:")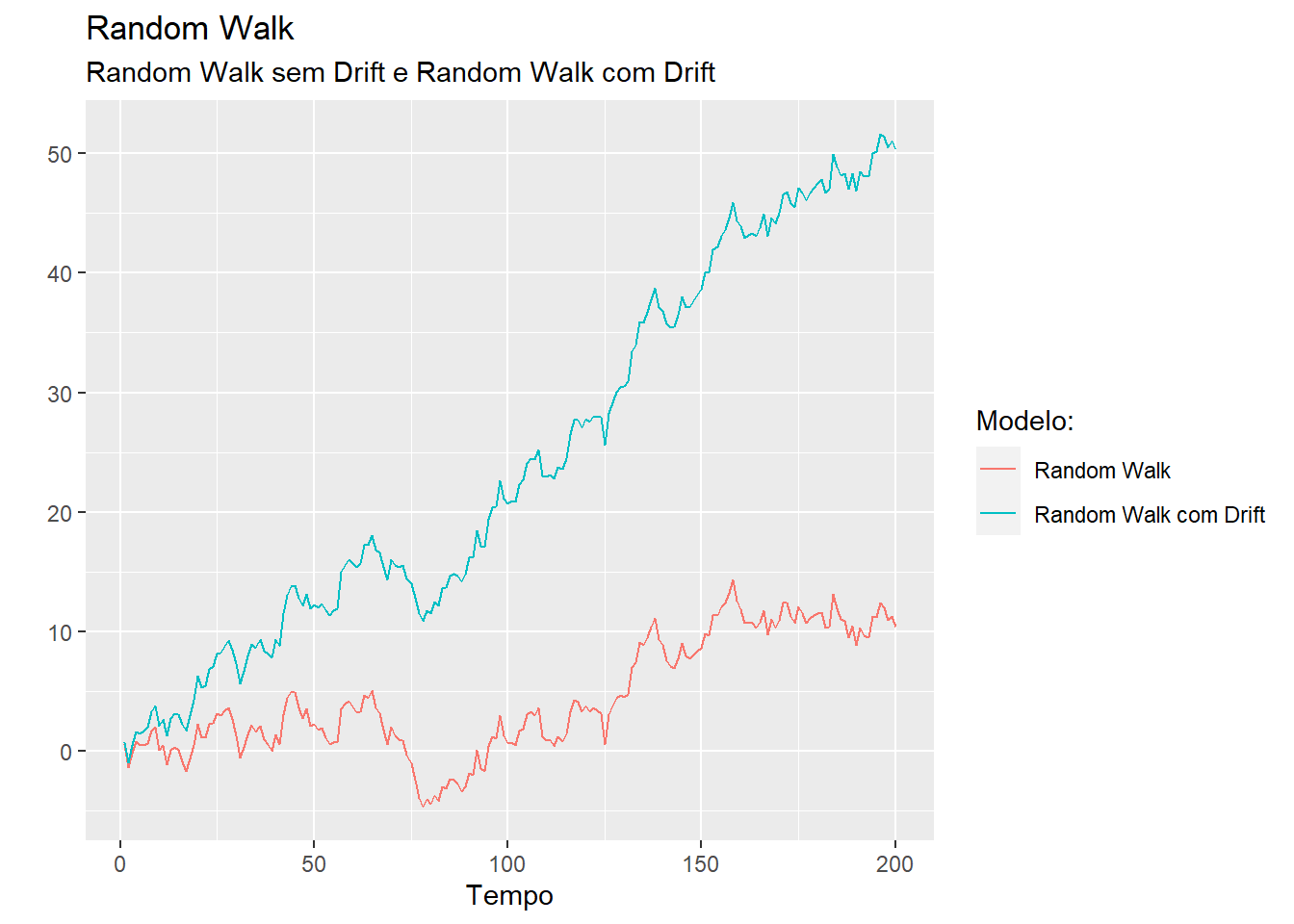

Figure 4.4: Série Temporal com Random Walk

4.5 Sinal no Ruído

Muitos modelos realistas para gerar séries temporais assumem um sinal com algum tipo de variação periódica que é contaminada pela adição de um ruído aleatório. Por exemplo, considere um modelo do tipo:

\[y_t = 2 \cos \left(2 \pi \frac{t + 15}{50}\right) + w_t\]

para \(t = 1,2,...,200\), onde o primeiro termo é o sinal. Abaixo temos um modelo aditivo simples na forma de \(y_t = s_t + w_t\), onde \(s_t\) denota algum sinal desconhecido e \(w_t\) denota um ruído branco. O problema de detectar um sinal e então extrair \(s_t\) é de grande interesse. Em economia, o sinal pode ser uma tendência ou um componente sazonal da série.

curva_onda = 2*cos(2*pi*1:200/50 + .6*pi)
df <- df %>% 
  mutate(curva_onda = curva_onda,
         curva_onda_ruido = curva_onda + ruido_branco,
         curva_onda_ruido_forte = curva_onda + 5*ruido_branco)


p1 <- df %>% 
  ggplot(aes(x = x, y = curva_onda)) +
  geom_line() +
  labs(title = "Curva em Onda", y = "", x = "")

p2 <- df %>% 
  ggplot(aes(x = x, y = curva_onda_ruido)) + 
  geom_line() +
  labs(title = "Curva em Onda  + Ruído", y = "", x = "")


p3 <- df %>% 
  ggplot(aes(x = x, y = curva_onda_ruido_forte)) +
  geom_line() +
  labs(title = "Curva em Onda + Ruído Forte", y = "", x = "")

  
gridExtra::grid.arrange(p1, p2, p3)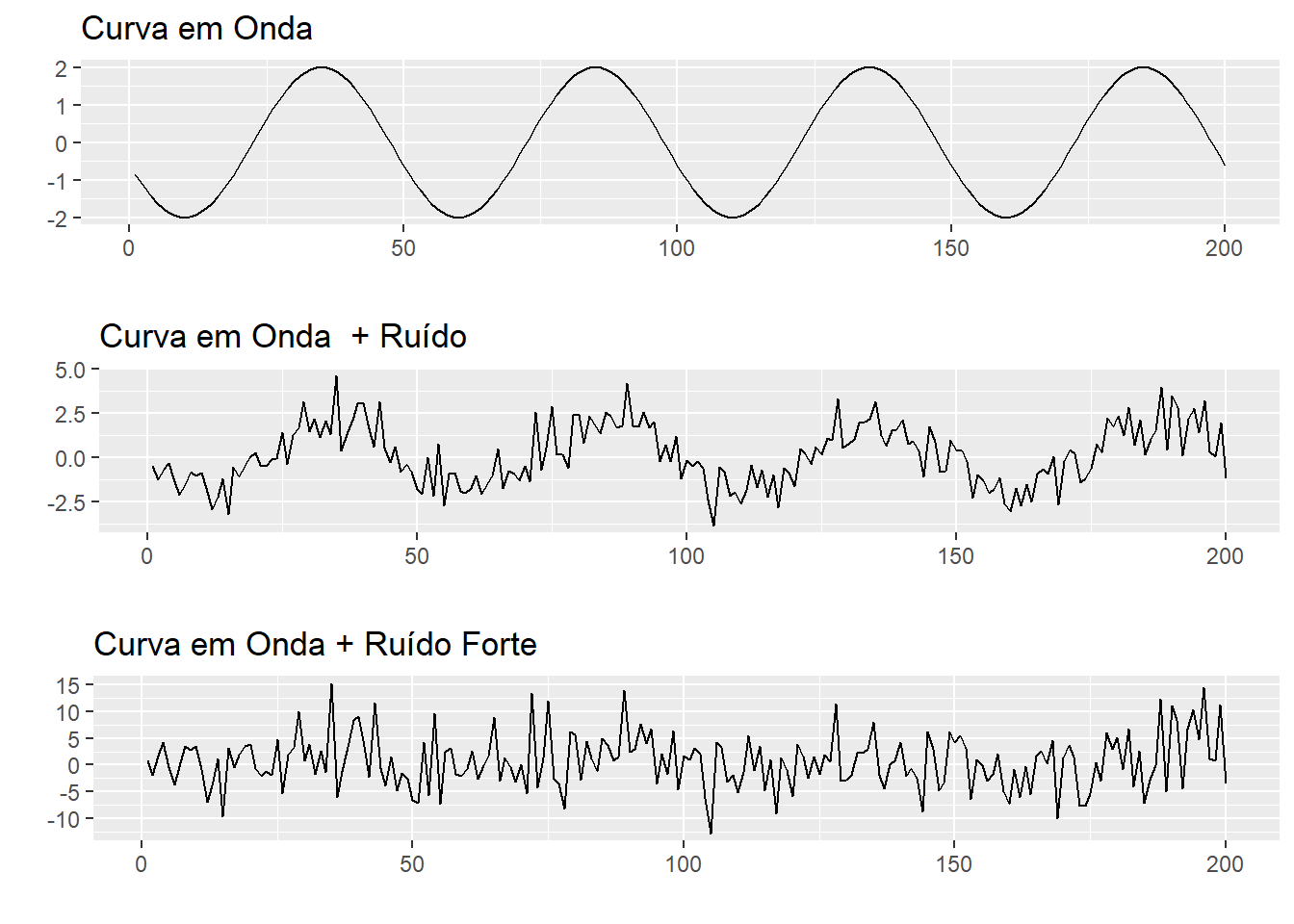

Figure 4.5: Séries Temporais com diferentes sinais