Capítulo 9 Modelos de Regressão Dinâmicos

O uso de variáveis explicativas exógenas é uma maneira óbvia de melhorar a precisão das precisões. Em vez de depender apenas de informações históricas sobre a série em si, podemos utilizar outras informações relevantes.

Modelos de séries temporais como ARIMA permitem que valores da série sejam previstos a partir da inclusão de informações do passado, mas não permitem a inclusão destas variáveis exógenas relevantes como dummies de feriado, atividade dos concorrentes, mudanças nas leis, variáveis macroeconômicas e outras covariadas externas que podem ajudar a explicar a variação histórica de uma série temporal.

Já modelos de regressão permitem a inclusão de variáveis externas, mas não são capazes de modelar as dinâmicas presentes em séries temporais, como os modelos ARIMA são capazes.

9.0.1 Valor de utilizar variáveis explicativas

Variáveis externas podem ser especialmente úteis para previsão de demanda por eletricidade, que é altamente dependente da temperatura ambiente, uma vez que dias quentes levam a maior uso de ar condicionados (Taieb and Hyndman 2014).

Contudo, nem sempre variáveis externas podem ser tão úteis. No caso de temperatura como uma variável explicativa para demanda por eletricidade, as previsões metereológicas podem fornecer medidas bem precisas do comportamento futuro, mas em casos onde as previsões das variáveis explicativas são imprecisas, adiciona-las ao modelo pode produzir resultados inconsistentes.

Outro problema pode ocorrer caso a relação entre \(y\) e \(x\) é um fato histórico, mas pode não se repetir no futuro. Ou quando duas variáveis possuem uma relação positiva em um período, e negativa em outro. Esse tipo de problema pode produzir modelos com má especificações e previsões imprecisas.

Assim, antes de recorrer a variáveis externas em modelos de séries temporais, é sempre interessante iniciar a análise com uma abordagem puramente de séries temporais (um modelo ARIMA, por exemplo). Outra estratégia e a de realizar comparações entre (1) uma previsão para dentro da amostra que inclua variáveis explicativas previstas e (2) uma previsão para dentro da amostra que inclua as mesmas variáveis explicativas com dados observados.

9.0.2 Modelos Dinâmicos de Regressão

Se existem previsões precisas para as variáveis explicativas e a relação entre estas variáveis e a previsão é estável no futuro, podemos utilizar uma abordagem mista que envolve extender os modelos ARIMA com o objetivo de permitir que outras variáveis externas sejam incluídas nos modelos. Assim, teriamos o melhor dos dois mundos.

Estes modelos de regressão simples tomam a forma

\[y_t = \beta_0 + \beta_1 x_{1,t} + ... + \beta_k x_{k,t} + \epsilon_t\]

onde \(y_t\) é uma função linear das \(k\) variáveis externas (\(x_{1,t},...,x_{k,t}\)), e \(\epsilon_t\) é assumido como um termos de erro não correlacionado (ruído branco). Testes como de Breusch-Godfrey foram utilizados para assegurar que os resíduos resultantes da regressão eram significativamente correlacionados.

Neste capítulo, os erros da regressão podem conter autocorrelação. Para enfatizar esta mudança, vamos substituir o uso do \(\epsilon_t\) por \(\eta_t\). A série de erros \(\eta_t\) é assumido como um processo ARIMA. Por exemplo, se \(\eta_t\) seguir um processo ARIMA(1,1,1), podemos escrever o modelo como

\[y_t = \beta_0 + \beta_1 x_{1,t} + ... + \beta_k x_{k,t} + \eta_t\]

\[(1-\Phi_1 B)(1-B)\eta_t = (1+ \theta_1 B) \epsilon_t\]

onde \(\epsilon_t\) é a série de ruído branco.

Note que o modelo tem dois termos de erro - o erro do modelo de regressão, que denotamos como \(\eta_t\). e o termo de erro do modelo ARIMA, que denotamos como \(\epsilon_t\). Apenas os erros do modelo ARIMA são assumidos como ruído branco.

9.1 Estimação

Quando estimamos parâmetros do modelo, minimizamos a soma de \(\epsilon_t\) ao quadrado. Se minimizarmos a soma de \(\eta_t\) ao quadrado (que é o que ocorre quando estimamos um modelo de regressão que ignora a autocorrelação dos erros), então uma série de problemas surgem.

1. Os coeficientes estimados \(\hat{\beta}_0,...,\hat{\beta}_k\) não são mais os melhores estimadores, já que algumas informações importantes estão sendo ignoradas no cálculo dos coeficientes.

2. Qualquer teste estatístico associado com o modelo será incorreto.

3. Os valores de AIC dos modelos ajustados não são um bom guia de quão bom é o modelo para previsão.

4. Na maioria dos casos, o p-valor associado com os coeficientes será muito pequeno, e algumas covariadas parecerão importantes quando na verdade não são. Isto produzirá uma regressão espúria.

Minimizar a soma dos \(\epsilon_t\) ao quadrado evita estes problemas. Alternativamente, estimação por máxima verossimilhança pode ser utilizada, produzindo estimativas de coeficientes similares.

Uma importante consideração quando estimando um modelo de regressão com erros ARMA é de que todas as variáveis do modelo devem ser estacionárias. Portanto, devemos primeiro checar se \(y_t\) é todas as covariadas são estacionárias. Se estimarmos o modelo quando qualquer uma delas é não-estacionária, os coeficientes produzidos não serão consistentes. Uma exceção é quando variáveis não-estacionárias são cointegradas. Se existe uma combinação linear de \(y_t\) não-estacionário com um \(x_t\) estacionário, então o coeficiente é consistente.

Para tornar as variáveis estacionárias, podemos realizar a transformação de diferenciação, o que produz o chamado “modelo em diferença”, em contraste com o “modelo em nível”, em os dados originais são utilizados.

Se todas as variáveis são estacionárias, então podemos utilizar erros ARMA para os resíduos. É fácil notar que uma regressão com erros ARIMA é equivalente a uma regressão em diferença com erros ARMA.

9.2 Regressão com Erros ARIMA

A função Arima() é capaz de ajustar um modelo de regressão com erros ARIMA se o argumento xreg for utilizado. Como a diferenciação está especificada, ela é aplicada para todas as variáveis antes de estimar o modelo. O comando R utilizado é

library(forecast)
Arima(y, xreg = x, order = c(1,1,0))

que irá ajustar um modelo do tipo \(y'_t = \beta_1 x'_t + \eta'_t\).

A função auto.arima() também é capaz de utilizar covariadas com uso do termo xreg. O usuário deve especificar os preditores e auto.arima() seleciona o melhor modelo ARIMA para os erros.

O pacote modeltime tem suporte ao modelo ARIMA com o uso da função arima_reg() ao se utilizar uma fórmula com regressor externo.

9.2.1 Exemplo: Consumo e Renda nos EUA

A figura 9.1 mostra a mudança trimestral nos gastos com consumo pessoal e a renda disponível entre 1970 e 2016. Estamos interessados em prever o consumo com base na renda. Uma mudança na renda não necessariamente reflete uma mudança instântanea no consumo (exempl, depois de uma demissão, pode levar alguns meses para os gastos se ajustarem). Contudo, vamos ignorar esta complexidade e tentar medir o efeito instantâneo de uma mudança média na renda sore uma mudança média nos gastos.

library(tidyverse)
library(tidymodels)
library(timetk)
library(modeltime)
library(fpp3)


us_change_df <- us_change %>% 
  tk_tbl() %>% 
  mutate(Quarter = as.Date(Quarter))

## Warning in tk_tbl.data.frame(.): Warning: No index to preserve. Object otherwise
## converted to tibble successfully.

us_change %>% 
  pivot_longer(cols = 2:6) %>% 
  filter(name %in% c("Consumption", "Income")) %>% 
  plot_time_series(Quarter, value, 
                   .facet_vars = name,
                   .facet_scales = "free_y",
                   .smooth = F,
                   .interactive = F,
                   .title = "")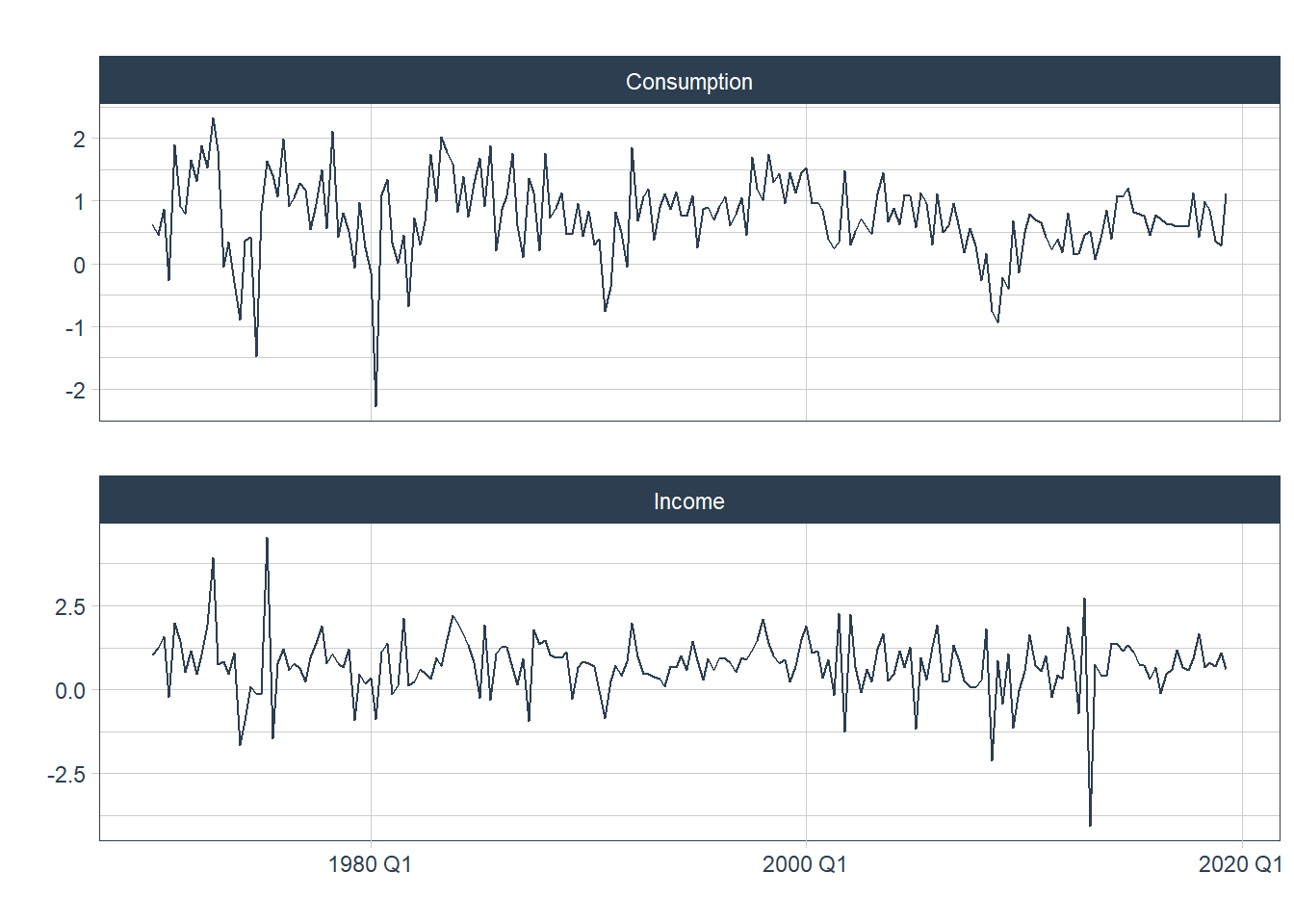

Figure 9.1: Mudança Percental no Consumo e Renda Trimestral para os EUA, 1970 a 2019

Vamos dividir a base em treinamento e teste para realizar a previsão proposta com a função initial_time_split(). Usando o parâmetro prop = 0.75, para utilizar 75% dos dados para a base de treinamento e 25% para a base de teste.

tbl_treinamento_teste <- 
  us_change_df %>% 
  initial_time_split(prop = 0.75)

tbl_treinamento_teste %>% 
  tk_time_series_cv_plan() %>% 
  plot_time_series_cv_plan(Quarter, 
                           Consumption,
                           .title = "",
                           .interactive = F)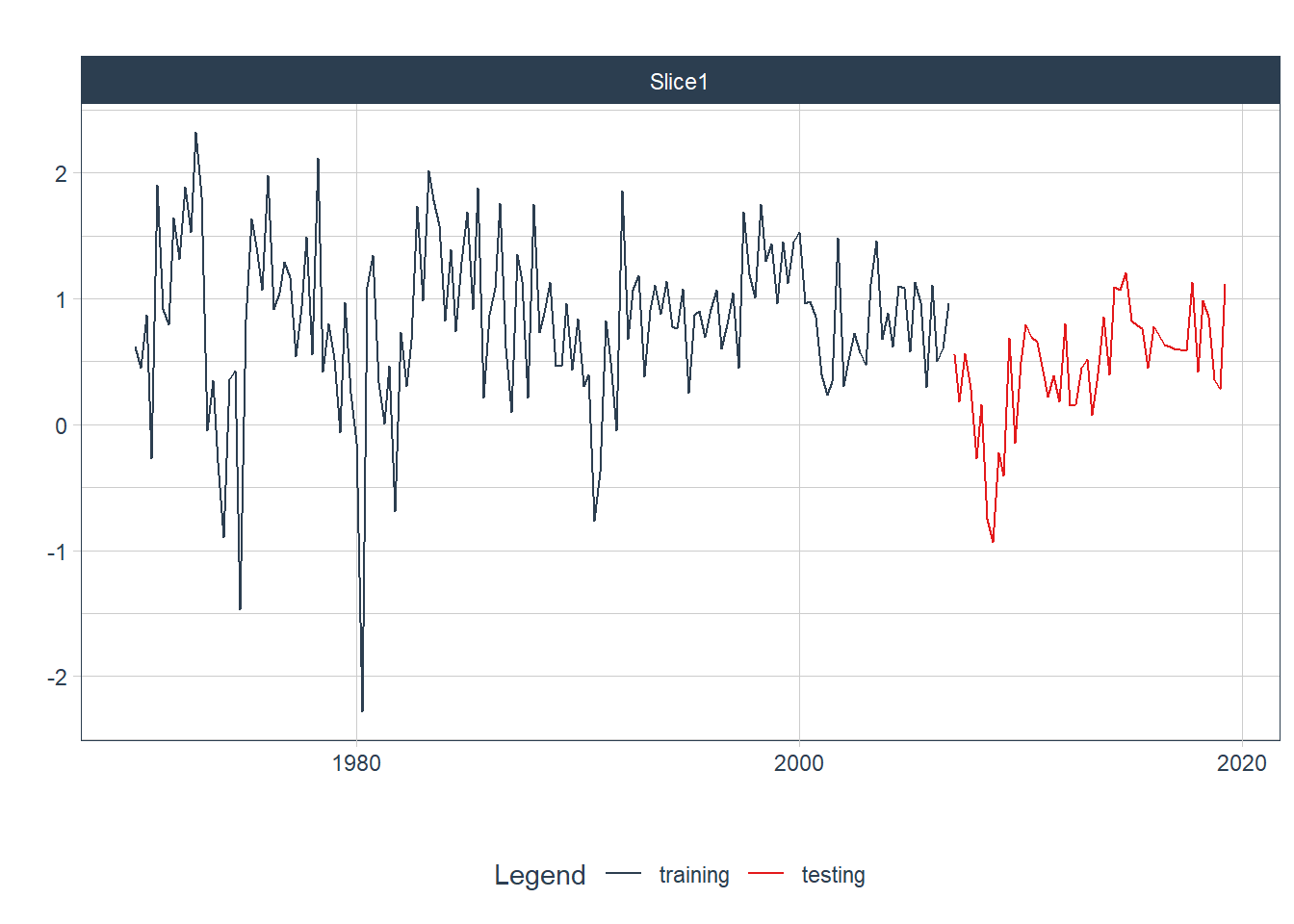

Figure 9.2: Base de Treinamento e Teste para dados de Consumo

Seguindo o fluxo de trabalho do pacote tidymodels, começamos criando o modelo com a função arima_reg() e a conectamos à função forecast::auto.arima() usando a expressão set_engine("auto_arima"). Não vamos fixar os parâmetros do modelo ARIMA, deixando a escolha para o pacote `auto.arima´, que escolhe os parâmetros de modo a minimizar critérios de informação.

Para estimar um modelo ARIMA convencional, poderiamos utilizar a fórmula Consumption ~ Quarter, mas como desejamos adicionar uma variável dependente adicional, vamos definir uma fórmula que toma Consumption como variável dependente e Income como um regressor.

modelo_regarima <- arima_reg() %>% 
  set_engine("auto_arima")

receita <- recipe(Consumption ~ Quarter + Income, training(tbl_treinamento_teste))

Com a função workflow unimos modelo e fórmula para realizar o ajuste do modelo. Abaixo temos a saída típica do ajuste do modelo que foi produzido para a base de treinamento.

fit <- workflow() %>% 
  add_model(modelo_regarima) %>% 
  add_recipe(receita) %>% 
  fit(training(tbl_treinamento_teste))

## frequency = 4 observations per 1 year

fit

## ══ Workflow [trained] ════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: arima_reg()
## 
## ── Preprocessor ──────────────────────────────────────────────────────────────
## 0 Recipe Steps
## 
## ── Model ─────────────────────────────────────────────────────────────────────
## Series: outcome 
## Regression with ARIMA(1,0,2) errors 
## 
## Coefficients:
##          ar1      ma1     ma2  intercept  income
##       0.5987  -0.5570  0.1840     0.6180  0.2725
## s.e.  0.1945   0.2016  0.0821     0.0886  0.0608
## 
## sigma^2 = 0.3545:  log likelihood = -130.8
## AIC=273.59   AICc=274.19   BIC=291.58

Os dados são claramente estacionários (já que estamos considerando mudanças percentuais em vez de gastos e renda bruta), de modo que não há necessidade de diferenciação. O modelo ajustado é

\[y_t = 0.6180 + 0.2725x_t + \eta_t\] \[\eta_t = 0.5987 \eta_{t-1} + \epsilon_t - 0.5570\epsilon_{t-1} + 0.1840 \epsilon_{t-2}\]

\[\epsilon \sim IID(0, 0.3545)\]

Podemos recuperar as estimativas de \(\eta_t\) e \(\epsilon_t\) usando a função residuals(). A figura 9.3 mostra que os resíduos do modelo parecem bem comportados, lembrando um processo de ruído branco.

tbl_calibracao <- 
  modeltime_calibrate(fit, 
                      new_data = testing(tbl_treinamento_teste))
  
  
tbl_calibracao %>% 
  modeltime_residuals() %>%  
  plot_modeltime_residuals(.title = "", 
                           .legend_show = F,
                           .interactive = F)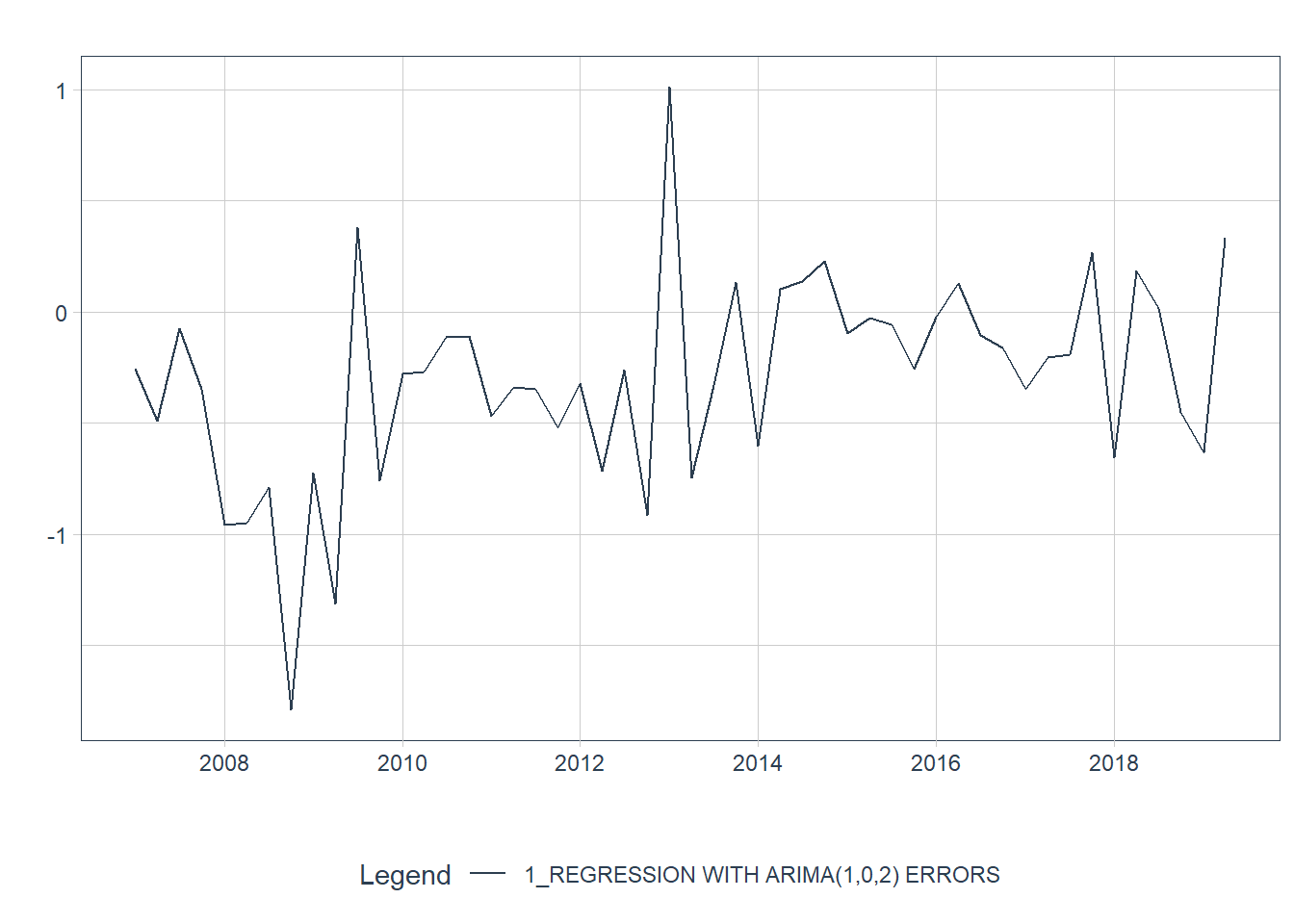

Figure 9.3: Resíduos de Regressão e Resíduos ARIMA para o modelo ajustado

Na figura 9.4 vemos o correlograma dos resíduos. As barras azuis indicam que as autocorrelações são indistinguíveis de um ruído branco.

tbl_calibracao %>% 
  modeltime_residuals() %>% 
  plot_modeltime_residuals(.type = "acf", .lag = 40,
    .title = "", 
    .interactive = FALSE,
    .show_white_noise_bar = T)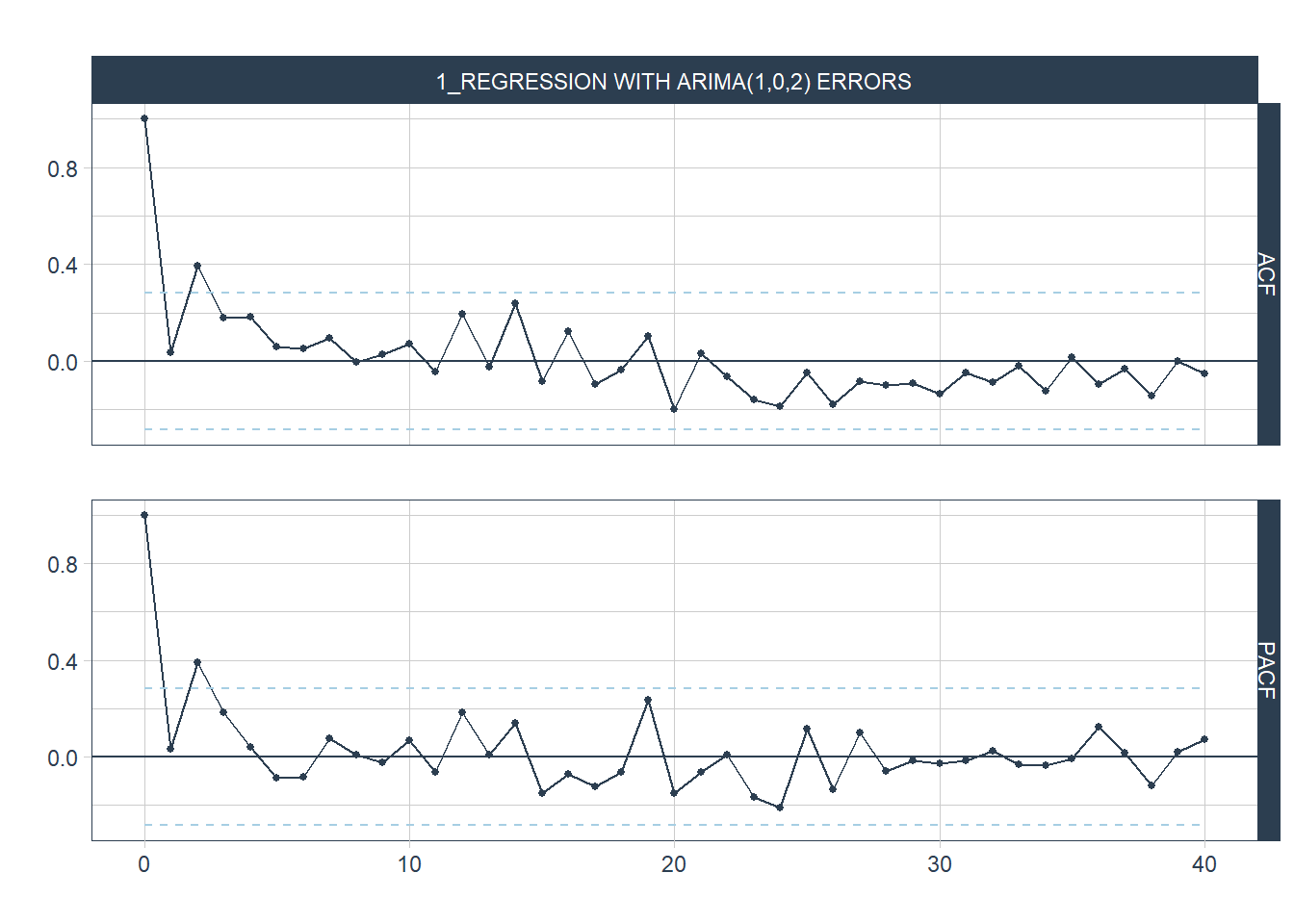

Figure 9.4: ACF dos Resíduos de Regressão e Resíduos ARIMA para o modelo ajustado

O teste de Ljung-Box, ACF e histograma parecem confirmar as informações do ACF, e indicam que os resíduos não são significativamente diferentes de um ruído branco.

A tabela 9.1 mostra o resultado para testes de normalidade e de autocorrelação dos resíduos. O teste de Shapiro-Wilk indica que os resíduos parecem normais. Os testes de Ljung-Box e Box-Pierce mostram que os resíduos não são significativamente diferentes de um ruído branco.

tbl_calibracao %>% 
  modeltime_residuals() %>% 
  modeltime_residuals_test() %>% 
  select(-.model_id, -.model_desc) %>% 
  knitr::kable(caption = "Testes para Resíduos do Modelo de Regressão com Erros ARIMA")

Table 9.1: Testes para Resíduos do Modelo de Regressão com Erros ARIMA

shapiro_wilk	box_pierce	ljung_box	durbin_watson
0.1814417	0.8089019	0.8032553	1.326655

9.3 Previsão

Para realizar previsões com modelo de regressão com Erros ARIMA, precisamos realziar a previsão da parte do modelo de regressão e a parte ARIMA do modelo. A figura 9.5 mostra a previsão feita para o período de teste. A linha azul mostra os dados reais e a linha vermelha, a previsão produzida pelo modelo.

tbl_calibracao %>% 
  modeltime_forecast(new_data = testing(tbl_treinamento_teste),
                     actual_data = us_change_df) %>% 
  plot_modeltime_forecast(.legend_show = F)

Figure 9.5: Previsão de Consumo do Modelo de Regressão com Erros ARIMA

É importante destacar que a previsão de valores futuros envolve a previsão de valores futuros para os preditores. Neste caso, teremos que modelar estas variáveis ou assumir valores para o período futuro. Assim, o intervalo de confiança produzido pela previsão não leva em consideração a incerteza adicional de ter que prever valores para os preditores, e devem ser interpretados como condicional aos valores assumidos.

Para finalizar, podemos calcular algumas medidas de performance. Os resultados são exibidos na tabela 9.2.

tbl_calibracao %>% 
  modeltime_accuracy(new_data = testing(tbl_treinamento_teste)) %>% 
  select(-.model_id, -.model_desc, -.type) %>% 
  knitr::kable(caption = "Medidas de Performance do Modelo de Regressão com Erros ARIMA")

Table 9.2: Medidas de Performance do Modelo de Regressão com Erros ARIMA

mae	mape	mase	smape	rmse	rsq
0.4186742	138.5321	1.232955	72.59967	0.5516429	0.0666645

Considerando que os dados de mudança percentual do consumo estão ao redor de zero, não é surpreendente que o valor calculado para o MAPE esteja tão elevado.

9.4 Exemplo 2: Previsão de Demanda por Eletricidade

vic_elec_daily <- vic_elec %>% 
  tk_tbl() %>% 
  filter(year(Time) == 2014) %>% 
  group_by(Date) %>% 
  summarise(
    Demand = sum(Demand) / 1e3,
    Temperature = max(Temperature),
    Holiday = any(Holiday)
  ) %>% 
  mutate(Day_Type = case_when(
    Holiday ~ "Feriado",
    wday(Date) %in% 2:6 ~ "Fim-de-semana",
    TRUE ~ "Dia-de-semana"
  ))

## Warning in tk_tbl.data.frame(.): Warning: No index to preserve. Object otherwise
## converted to tibble successfully.

vic_elec_daily %>% 
  pivot_longer(c(Demand, Temperature)) %>% 
  plot_time_series(Date, value,
                   .facet_vars = name,
                   .title = "",
                   .smooth = F)

Figure 9.6: Demanda por Eletricidade diária e temperatura máxima apara o Estado de Vitoria na Australia, 2014

A figura 9.7 mostra que existe uma relação não linear entre temperatura e demanda por eletricidade. Essa relação se altera a depender do tipo de dia: durante os fins de semana, a demanda por eletricidade é maior, mesmo quando controlamos por temperatura.

vic_elec_daily %>% 
  ggplot(aes(x = Temperature, y = Demand, colour = Day_Type)) +
  geom_point() + 
  labs(y = "Demanda por Eletricidade (GW)",
       x = "Temperatura Máxima",
       color = "Dia da Semana")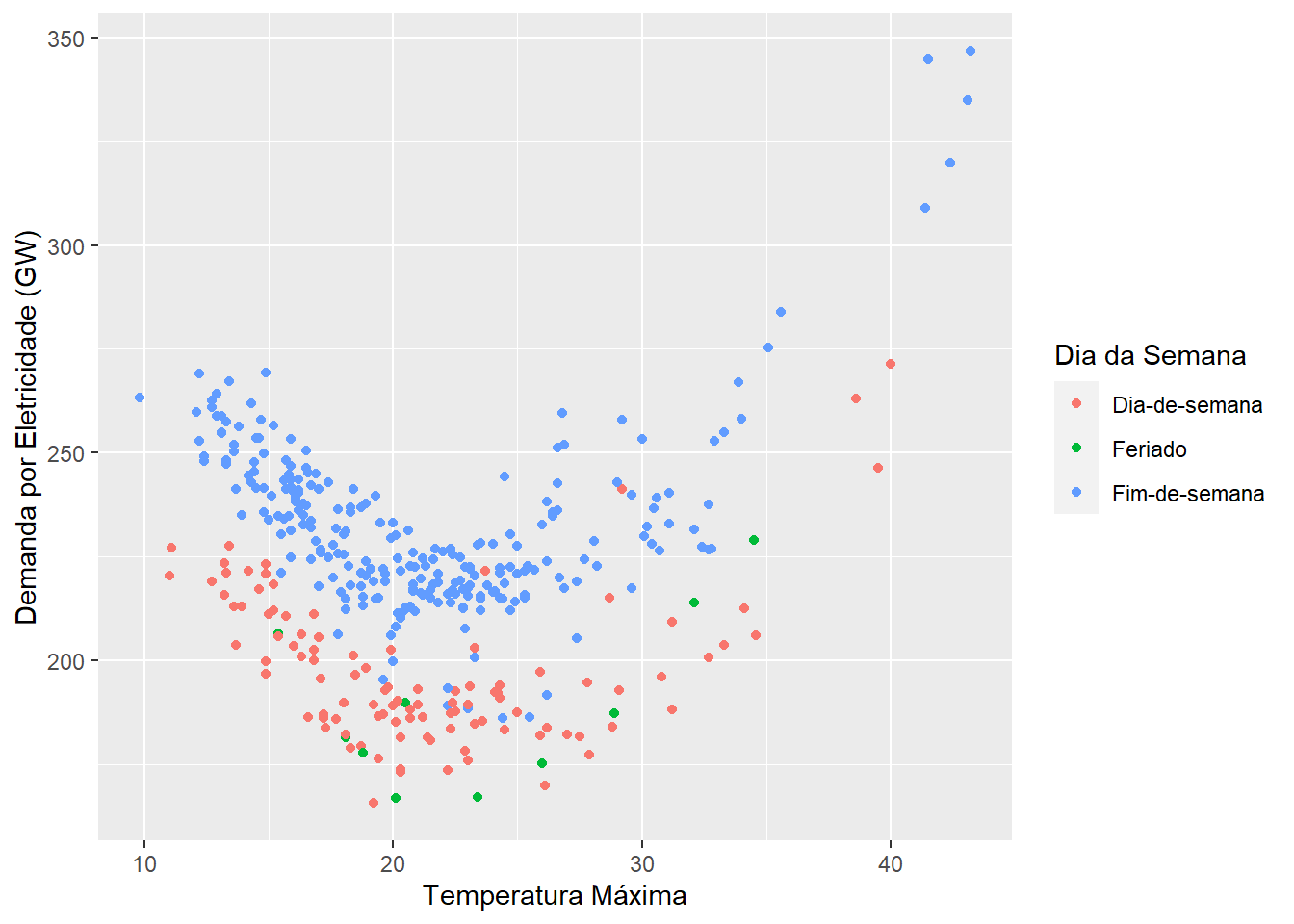

Figure 9.7: Relação entre demanda diária por eletricidade e temperatura para o Estado de Vitória na Australia, 2014

Abaixo criamos os conjuntos de treinamento e teste e definimos a fórmula a ser estimada. Como a relação entre temperatura e demanda por energia elétrica é não linear, utilizamos a função step_poly para criar variáveis utilizando polinômios ortogonais. Com step_dummy criamos variáveis indicativas para os feriados e fim de semana.

elec_splits <- vic_elec_daily %>% 
  initial_time_split(prop = 0.75)


receita_elec <- recipe(Demand ~ ., data = training(elec_splits)) %>% 
  step_rm(Holiday) %>% 
  step_dummy(Day_Type) %>% 
  step_poly(Temperature)

receita_elec %>% prep() %>% bake(new_data = NULL)

## # A tibble: 273 × 6
##    Date       Demand Day_Type_Feriado Day_Type_Fim.de.semana Temperat…¹ Temper…²
##    <date>      <dbl>            <dbl>                  <dbl>      <dbl>    <dbl>
##  1 2014-01-01   175.                1                      0    0.0519  -0.0544 
##  2 2014-01-02   188.                0                      1    0.0234  -0.0547 
##  3 2014-01-03   189.                0                      1    0.0159  -0.0517 
##  4 2014-01-04   174.                0                      0   -0.00212 -0.0393 
##  5 2014-01-05   170.                0                      0    0.0528  -0.0541 
##  6 2014-01-06   195.                0                      1   -0.00875 -0.0330 
##  7 2014-01-07   200.                0                      1   -0.00496 -0.0367 
##  8 2014-01-08   205.                0                      1    0.0651  -0.0481 
##  9 2014-01-09   227.                0                      1    0.112    0.00669
## 10 2014-01-10   258.                0                      1    0.128    0.0349 
## # … with 263 more rows, and abbreviated variable names ¹​Temperature_poly_1,
## #   ²​Temperature_poly_2

Abaixo temos o modelo ajustado para previsão de energia elétrica.

fit_elec <- workflow() %>% 
  add_model(modelo_regarima) %>% 
  add_recipe(receita_elec) %>% 
  fit(training(elec_splits))

## frequency = 7 observations per 1 week

fit_elec 

## ══ Workflow [trained] ════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: arima_reg()
## 
## ── Preprocessor ──────────────────────────────────────────────────────────────
## 3 Recipe Steps
## 
## • step_rm()
## • step_dummy()
## • step_poly()
## 
## ── Model ─────────────────────────────────────────────────────────────────────
## Series: outcome 
## Regression with ARIMA(2,0,1)(0,0,2)[7] errors 
## 
## Coefficients:
##          ar1      ar2      ma1    sma1    sma2  intercept  day_type_feriado
##       1.2865  -0.3586  -0.4817  0.1527  0.3246   200.1825            3.6693
## s.e.  0.6723   0.5746   0.6511  0.0690  0.0579     4.2842            2.1880
##       day_type_fim_de_semana  temperature_poly_1  temperature_poly_2
##                      33.3701            149.4592            186.9024
## s.e.                  1.2064             11.8570              9.4430
## 
## sigma^2 = 45.8:  log likelihood = -905.87
## AIC=1833.73   AICc=1834.74   BIC=1873.44

\[y_t = 200.18 + 3.66 \text{feriado}_t + 149.46 \text{temperatura_1}_t + 186.90 \text{temperatura_2} + \eta_t\]

tbl_calibracao_elec <- fit_elec %>% 
  modeltime_calibrate(new_data = testing(elec_splits))


tbl_calibracao_elec %>% 
  modeltime_residuals() %>% 
  plot_modeltime_residuals(.type = "acf", .show_white_noise_bar = T, .lag = 21)

tbl_calibracao_elec %>% 
  modeltime_forecast(new_data = testing(elec_splits),
                     actual_data = vic_elec_daily) %>% 
  plot_modeltime_forecast(.legend_max_width = 10)

tbl_calibracao_elec %>% 
  modeltime_accuracy(new_data = testing(elec_splits)) %>% 
  table_modeltime_accuracy()

## Warning: `bindFillRole()` only works on htmltools::tag() objects (e.g., div(),
## p(), etc.), not objects of type 'shiny.tag.list'.

9.5 Regressão com Termos Harmônicos

Modelos ARIMA tendem a produzir resultados interessantes com séries mensais, trimestrais e anuais. O modelo ETS atribui pesos exponencialmente decrescentes aos valores defasados da série para estimar seus valores atuais, e funcionam bem com dados diários, mensais e anuais. Para séries diárias, se o período de análise compreende mais de um ano, é possível que além da sazonalidade semanal usual destes dados (frequência de 7), em que existe uma relação entre os dias da semana, seja preciso permitir a presença de sazonalidade anual. Nesta situação o modelo ETS produzirá resultados inconsistentes.

O problema é ainda maior para dados semanais. Segundo Hyndman, criador do pacote forecast, modelos ARIMA e ETS tem dificuldades em produzir boas previsões para séries semanais devido a sua sazonalidade peculiar, dado que o período de sazonalidade é de em média \(365,25/7 = 52,18\). Como estes modelos só aceitam valores inteiros para a frequência, mesmo um valor aproximado de 52 períodos pode gerar resultados inadequados.

Seja com dados diários muito longos ou para dados semanais, uma alternativa é o uso do modelo TBATS. Este modelo é uma extensão do ETS que adiciona uma série de transformações Box-Cox, séries Fourier com coeficientes variantes no tempo além de correção de erro ARMA. Ele é especialmente útil para produzir previsão de séries temporais com múltiplos períodos de sazonalidade, sazonalidade de altíssima-frequência, sazonalidade não-inteira (como a frequência de 52,18 discutida acima) e múltiplos efeito calendários.

Outra solução é utilizar termos de Fourier que são úteis em lidar com sazonalidade. Uma forma de utilizar estes termos é estimando modelos que aceitam covariadas externas como parte da especificação. É o caso do modelo de Regressão com Erros ARIMA. De modo geral, uma das principais vantagens da Regressão com Erro ARIMA é que os coeficientes das covariadas tem a interpretação usual dos modelos de regressão.

Em resumo, termos harmônicos tem as vantagens de:

• Permitir sazonalidades de qualquer comprimento;

• Permite modelar dados com mais de um período de sazonalidades;

• É possível controlar a suavização do padrão sazonal a partir do número de pares de termos seno e cosseno de Fourier;

• A dinâmica de curto prazo pode ser modelada pelo erro ARMA.

9.6 Exemplo:

acidentes <- read_rds("resources/acidentes_estradas_brasil.rds") %>% 
    filter_by_time(
    .start_date = last(Date) %-time% "12 month",
    .end_date = "end"
  ) 

## .date_var is missing. Using: Date

acidentes_split <- acidentes %>%
  time_series_split(date_var = Date,
                    assess = "4 months",
                    cumulative = TRUE
  )

acidentes_split %>%
  tk_time_series_cv_plan() %>%
  plot_time_series_cv_plan(Date, acidentes, .title = "")

Figure 9.8: Acidentes diários em rodovias federais, 2007 a 2021

Como discutido na seção 2, a série de acidentes possui um forte componente de sazonalidade associado ao dia da semana, mas também ao dia do mês.

receita_K1 <- recipe(acidentes ~ ., training(acidentes_split)) %>% 
  step_fourier(Date, period = c(7), K = 1)

receita_K2 <- recipe(acidentes ~ ., training(acidentes_split)) %>% 
  step_fourier(Date, period = c(7), K = 2)

receita_K3 <- recipe(acidentes ~ ., training(acidentes_split)) %>% 
  step_fourier(Date, period = c(7), K = 3)

modelo_arima <- arima_reg() %>% 
  set_engine("auto_arima")

wflw_acidentes_K1 <- workflow() %>% 
  add_model(modelo_arima) %>% 
  add_recipe(receita_K1) %>% 
  fit(training(acidentes_split))

## frequency = 7 observations per 1 week

wflw_acidentes_K2 <- workflow() %>% 
  add_model(modelo_arima) %>% 
  add_recipe(receita_K2) %>% 
  fit(training(acidentes_split))

## frequency = 7 observations per 1 week

wflw_acidentes_K3 <- workflow() %>% 
  add_model(modelo_arima) %>% 
  add_recipe(receita_K3) %>% 
  fit(training(acidentes_split))

## frequency = 7 observations per 1 week

tbl_modelos <- 
  modeltime_table(wflw_acidentes_K1,
                wflw_acidentes_K2,
                wflw_acidentes_K3) %>% 
  update_model_description(1, "ARIMA com Termos Harmônicos K = 1") %>% 
  update_model_description(2, "ARIMA com Termos Harmônicos K = 2") %>% 
  update_model_description(3, "ARIMA com Termos Harmônicos K = 3") 

tbl_calibracao <- tbl_modelos %>% 
  modeltime_calibrate(new_data = testing(acidentes_split)) 

tbl_calibracao %>% 
  modeltime_forecast(new_data = testing(acidentes_split),
                     actual_data = acidentes) %>% 
  filter_by_time(.start_date = last(.index) %-time% "4 month",
                 .end_date = "end") %>% 
  plot_modeltime_forecast(
                          .facet_vars = .model_desc, 
                          .facet_ncol = 2,
                          .title = "",
                          .legend_show = F)

## .date_var is missing. Using: .index

tbl_calibracao %>% 
  modeltime_accuracy(new_data = testing(acidentes_split)) %>% 
  table_modeltime_accuracy()

## Warning: `bindFillRole()` only works on htmltools::tag() objects (e.g., div(),
## p(), etc.), not objects of type 'shiny.tag.list'.

References

Taieb, Souhaib Ben, and Rob J Hyndman. 2014. “A Gradient Boosting Approach to the Kaggle Load Forecasting Competition.” International Journal of Forecasting 30 (2): 382–94.