Capítulo 6 Considerações Práticas

Neste capítulo vamos discutir alguns aspectos do processo de criação de previsões de séries temporais.

Na seção 6.1 vamos analisar como é possível criar conjuntos de teste e treinamento a partir de dados de séries temporais. Ao separar os dados em séries em períodos de treinamento e teste, podemos comparar valores previstos por um modelo com valores reais que não foram utilizados durante o processo de treinamento. Uma boa previsão para fora da amostra garante que o modelo é capaz de generalizar bem o comportamento da série, e não está apenas memorizando certos comportamentos. Este procedimento é facilitado com o uso do pacote rsample.

Na seção 6.2 vamos entender que antes de estimar os modelos de previsão, um extensivo processo de ajuste dos dados pode ser crucial para produzir bons resultados. Este processo passar pela identificação e correção de valores extremos (outliers), por ajustes em dados faltantes (missing values), criação de variáveis como dummies de feriado ou a transformação da variável original para sua versão em logarítimo. Cada uma dessas escolhas exige do analista a capacidade de ponderar prós e contras e um íntimo conhecimento dos dados utilizados. O pacote recipes fornece uma séries de funções convenientes para o ajuste dos dados.

Na seção 6.3 vamos mostrar como podemos utilizar o pacote modeltime para ajustar dois modelos simples de séries temporais.

Após o ajuste do modelo, uma análise dos resíduos é importante para avaliar a qualidade do modelo ajustado. Na seção 6.4 vamos investigar como a análise de normalidade dos resíduos e a autocorrelação podem nos ajudar na busca por um modelo com bom ajuste.

Na seção 6.5 vamos discutir como medir a performance de um modelo de previsão a partir dos seus erros de previsão. Para tanto, vamos analisar asss principais medidas utilizadas e como implementa-las no nosso workflow utilizando o pacote yardstick.

Por fim, na seção 6.6 vamos investigar o papel dos métodos de reamostragem no processo de previsão de séries temporais.

6.1 Conjuntos de teste e treinamento

A capacidade de um modelo de generalizar só pode ser realmente avaliada quando fazemos previsões de casos novos, para os quais o modelo não foi inicialmente treinado.

Uma opção bastante utilizada é a de dividir os dados em dois subconjuntos: conjunto de treinamento e conjunto de teste. O modelo é treinado nos conjuntos de treinamento e testado em novos casos, chamado de conjunto de teste. Podemos então comparar as previsões do modelo com os casos de teste e construir medidas de erro, que irão indicar se o modelo funciona bem para observações inéditas.

A figura 6.1 mostra uma série temporal separada em bases de treinamento e teste.

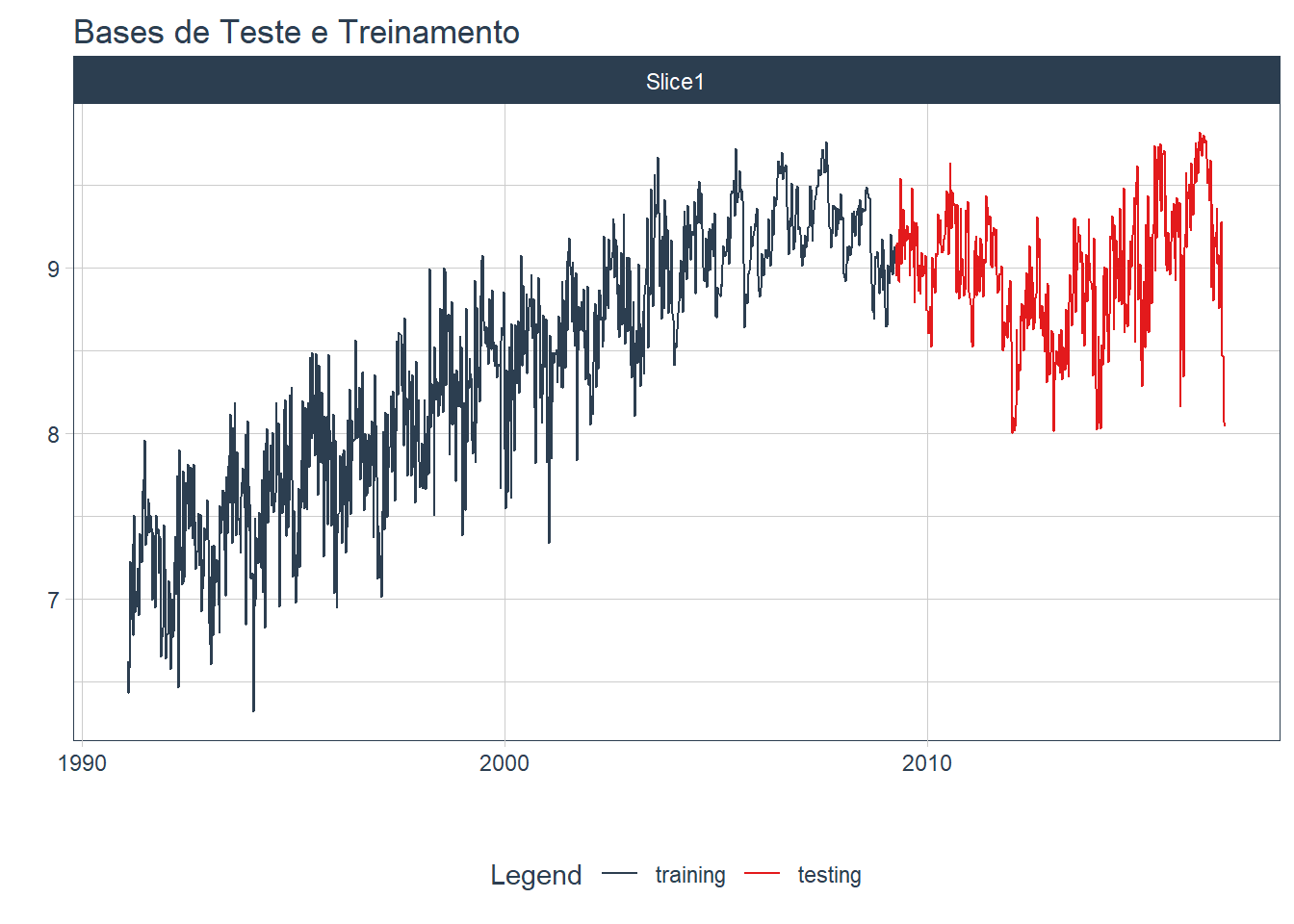
Figure 6.1: Separação de uma série temporal em base de treinamento e de teste

Na porção azul da figura, chamada de base de treinamento, o modelo de previsão é treinado. A partir desse modelo treinado, faremos previsões para o período de teste (vermelho), que são observações inéditas para o modelo, mas são informações conhecidas para o usuário. No exemplo acima, a base de teste é de 30% da série total. Como regra de bolso podemos definir o tamanho da base de teste em ao menos 20% dos dados totais.

Um modelo que possui uma boa performance na própria base de treinamento não necessariamente será capaz de realizar boas previsões para casos inéditos. O modelo pode estar sobreajustando os dados de treinamento, e memorizando o comportamento do período de treinamento, mas sendo incapaz de generalizar bem para novos casos.

6.1.1 Funções para dividir uma série temporal

Na figura 6.2 podemos visualizar os dados de oferta semanal de gasolina para os EUA. Estes dados são parte do pacote fpp3.

library(tidymodels) # contém o pacote rsample, yardstick e recipes
library(fpp3) # contém os dados us_gasoline
library(timetk)

data("us_gasoline")

us_gasoline <- us_gasoline %>%
  tk_tbl() %>% 
  mutate(Week = as.Date(Week))

## Warning in tk_tbl.data.frame(.): Warning: No index to preserve. Object otherwise
## converted to tibble successfully.

us_gasoline %>% 
  plot_time_series(Week, Barrels,
                   .title = "Oferta semanal de produtos de gasolina, EUA",
                   .y_lab = "Milhões de barril")

Figure 6.2: Oferta semanal de produtos de gasolina, EUA

No código acima, carregamos o pacote tidymodels (que contém os pacotes rsample, recipes e yardstick que serão utilizados ao longo do capítulo). Carregamos ainda o pacote timetk, que possui funções convenientes para tratamento de séries temporais, como a função tk_tbl(), que converte o objeto ts para data.frame.

Para separar os dados em base de treinamento e teste, vamos utilizar o pacote rsample. Com a função initial_split() podemos criar bases aleatórias de treinamento e teste. Contudo, para uma série temporal, como a estrutura temporal dos dados é importante, em vez de uma seleção aleatória dos valores que farão parte do conjunto de teste e do conjunto de treinamento, vamos definir estes conjuntos a partir de faixas temporais. Especificamente, vamos definir que a base de treinamento corresponderá aos primeiros 70% das observações, totalizando 948 observações.

gasoline_split <- us_gasoline %>%
  initial_time_split(prop = 0.7) 

gasoline_split

## <Training/Testing/Total>
## <948/407/1355>

O objeto gasoline_split é uma lista com informações dos dados de treinamento e de teste. Podemos utilizar as funções training() e testing do pacote rsample para acessar apenas as observações referentes aquela faixa específica. Abaixo, temos um resumo dos dados de teste utilizando a função testing(gasoline_split). Observe que as observações só tem inicio em abril de 2009.

testing(gasoline_split) %>% 
  head()

## # A tibble: 6 × 2
##   Week       Barrels
##   <date>       <dbl>
## 1 2009-04-06    8.94
## 2 2009-04-13    9.14
## 3 2009-04-20    9.15
## 4 2009-04-27    8.92
## 5 2009-05-04    8.91
## 6 2009-05-11    9.23

Podemos ainda visualizar como o período de treinamento e teste utilizando as funções tk_time_series_cv_plan() e plot_time_series_cv_plan(), que preparam os dados e visualizam o plano de teste e treinamento (figura 6.3).

df_treinamento <- training(gasoline_split)
df_teste <- testing(gasoline_split)

gasoline_split %>% 
    tk_time_series_cv_plan() %>% 
    plot_time_series_cv_plan(Week, Barrels, 
                             .title = "Bases de Teste e Treinamento",
                             .interactive = FALSE,
                             #.line_alpha = 0.5,
                             .line_type = 1,
                             ) 

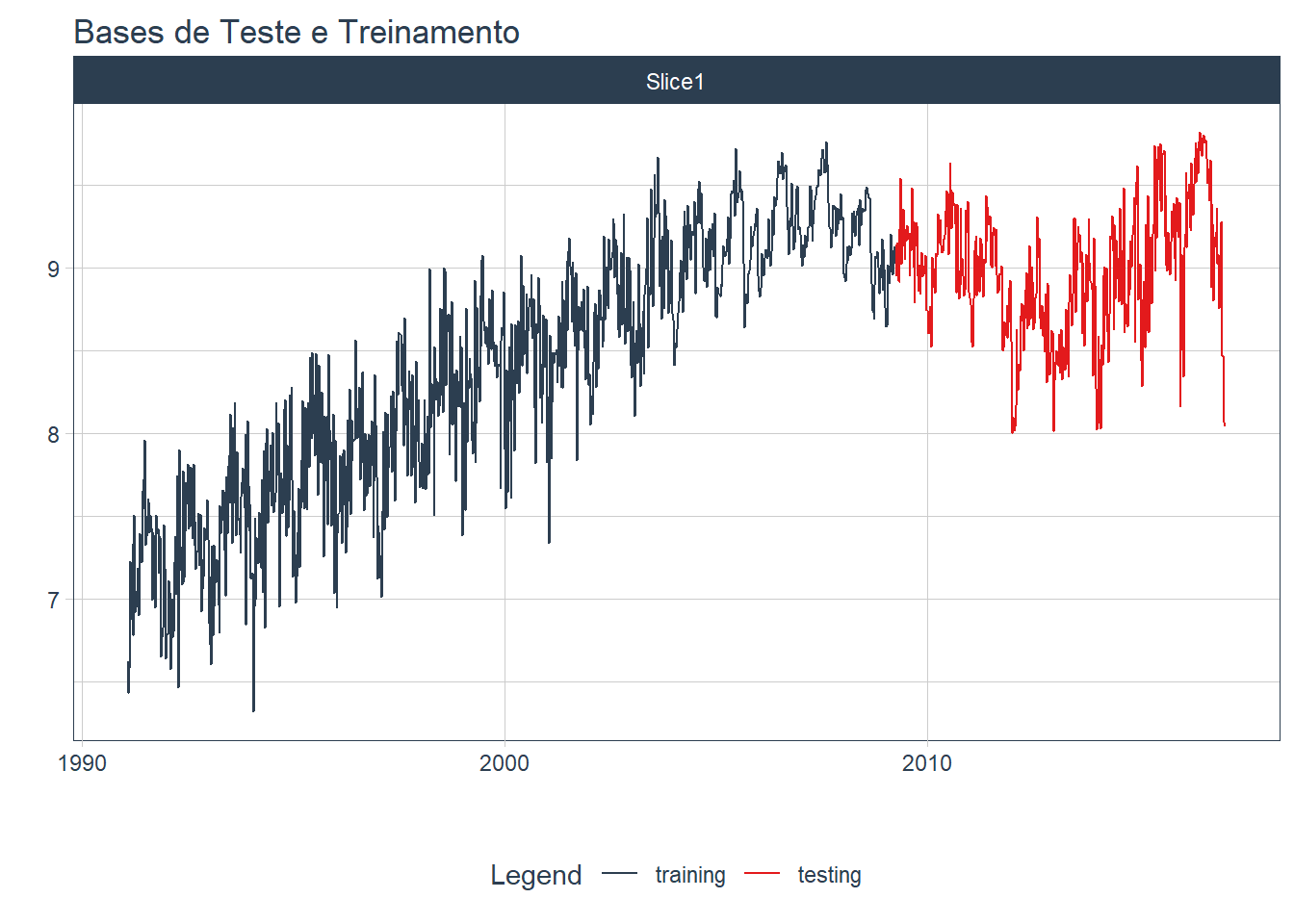
Figure 6.3: Bases de Teste e Treinamento para dados de gasolina, EUA

Na seção 6.3 vamos utilizar a base de treinamento criada acima para estimar alguns modelos de séries temporais. Na seção 6.5, utilizaremos a base de teste para avaliar os erros cometidos por estes modelos.

6.2 Transformação de variáveis

Melhorias das previsões podem ser obtidas pela transformação das séries originais. Dados de total de vendas mensais podem ser afetados por efeitos calendários (meses com mais dias possuem naturalmente mais vendas totais). Uma forma de corrigir esta distorção é trabalhar com a média diária de vendas para cada mês.

Dados agregados como produto interno bruto, total de empresas em uma cidade, total de leitos ou número de homicídios são distocidos por um efeito população. Uma transformação bastante popular é o de substituir a variável original por uma medida per capita.

Quando trabalhamos com variáveis monetárias como faturamento e arrecadação, ajustes pela inflação são fundamentais para realizar comparações justas ao longo do tempo. Para realizar este ajuste, é necessário utilizar um índice de inflação apropriado.

Outras transformações úteis incluem transformações matemáticas, como a mudança da série original para sua versão logarítima. Para uma série original \(y_1,...,y_T\), uma transformação logarítima tomará a forma \(w_t = \log(y_t)\). Este tipo de transformação pode ser útil pela sua interpretabilidade, já que mudanças em um valor log são mudanças percentuais na escala original. Se o log na base 10 é utilizado, um aumento de 1 na escala log corresponde a multiplicar a variável original por 10. Contudo, se a variável original possui valores zero ou negativos, este tipo de transformação não é possível.

Podemos ainda estar interessados em adicionar variáveis indicativas (dummies) para dia da semana, dia do mês ou feriados importantes no ano. Com isto, podemos capturar algum efeito sazonal ou efeito de calendário que não seria possível sem a adição destas variáveis. Dummies podem ainda ser utilizadas para indicar que determinadas observações são outliers, ou seja, representam desvios significativos do padrão normal da série temporal.

Por fim, a série temporal a ser prevista pode estar incompleta. Essas informações faltantes (missing values) podem ser preenchidas com a utilização de métodos de imputação de dados. Contudo, utilizar métodos de imputação exige do analista um profundo conhecimento dos dados. Se os dados faltantes são aleatórios ou muito próximo disso, a imputação simples dos dados não oferece custos importantes.

6.2.1 Funções para transformar dados

Antes de aplicar qualquer modelo aos dados, podemos utilizar o pacote recipes (parte do pacote tidymodels) para criar pequenas receitas de bolo com instruções de pré-processamento dos dados. Ele torna simples tarefas como a criação de variáveis dummies, a normalização de variáveis numéricas, a criação de variáveis derivadas da coluna de tempo (como dummy de dia, mês, ano e dia da semana), além de muitas outras operações de feature engineering que são tão importantes, mas por vezes tediosas.

Trabalhando com a base de dados us_gasoline, vamos converter os dados originais para sua versão logarítima. Primeiro, com a função recipe podemos utilizar uma fórmula para indicar a variável dependente e as variáveis independentes. No caso de uma série temporal univariada, a coluna de tempo (Week) pode ser incluida como variável independente. Precisamos ainda indicar qual a base a ser transformada, que será a base de treinamento.

receita_gasolina <- us_gasoline %>% recipe(Barrels ~ Week, training(gasoline_split))
receita_gasolina

## Recipe
## 
## Inputs:
## 
##       role #variables
##    outcome          1
##  predictor          1

Agora podemos realizar as transformações desejadas. Primeiro vamos utilizar a função step_log para criar uma versão log da variável dependente, que é selecionada a partir da função selecionadora all_outcomes (alternativamente podemos utilizar o nome da variável).

Outros seletores específicos do pacote recipe são: all_numeric_predictors(), all_numeric(), all_predictors() e all_outcomes.

receita_gasolina <- receita_gasolina %>% 
  step_log(all_outcomes()) 

Na tabela @ref(tab:tab_gasolina_log) vemos como a função recipe transformou a coluna Barrels para formato log.

receita_gasolina %>% 
  prep() %>% 
  juice() %>% 
  head() %>% 
  knitr::kable()

Week	Barrels
1991-02-04	1.890246
1991-02-11	1.861441
1991-02-18	1.884339
1991-02-25	1.977409
1991-03-04	1.927892
1991-03-11	1.938310

O pacote recipe permite outras transformações a partir de funções como step_meanimpute, step_sqrt(), step_BoxCox(), step_mutate(), step_cut()e step_date(). Uma lista de todas as transformações possíveis pode ser obtida na documentação do recipe.

6.3 Rodando um modelo simples

Nas próximas seções veremos modelos mais complexos e mais apropriados para os dados utilizados. Por enquanto, vamos utilizar alguns modelos simples, que podem servir como benchmarking para os modelos por vi.

6.3.1 Método da Média

Para este modelo, a previsão de todos os valores futuros é igual a média dos dados históricos. Se deixarmos os dados históricos serem denotados por \(y_1,...,y_T\), então os valores futuros serão dados como

\[\hat{y}_{T+h|T} = \bar{y}=\frac{y_1 + ... +y_T}{T}\]

A notação \(\hat{y}_{T+h|T}\) pode ser entendido como estimação de \(\hat{y}_{T+h}\) baseada nos dados de \(y_1,...,y_T\).

6.3.2 Método Naïve

Para previsões naïve, fazemos a previsão baseada no valor da última observação. Assim,

\[\hat{y}_{T+h|T} = y_T\]

A previsão naïve pode ser ótima quando temos dados de passeio aleatório.

6.3.3 Método Naïve Sazonal

É um método útil para dados sazonais. Neste caso, cada valor previsto é igual ao último valor observado do mesmo período sazonal do ano (ou o mesmo mês do ano anterior). Formalmente, a previsão para o tempo \(T+h\) é escrita como

\[\hat{y}_{T+h|T} = y_{T+h-m(k+1)}\] onde \(m=\text{período sazonal}\), e \(k\) é a parte inteira de \((h-1)/m\) (exemplo, o número de anos completos no período de previsão antes do tempo \(T+h\)). Assim, com dados mensais, a previsão para todos os meses de fevereiro serão iguais ao valor do último fevereiro observad. Com dados trimestrais, a previsão de todos os segundos trimestres serão iguais ao último segundo trimestre observado.

6.3.4 Função para ajustar modelos: parsnip

Finalmente, após as etapas de pré-processamento dos dados e a criação de um conjunto de treinamento e teste podemos utilizar o pacote parsnip para estimar alguns modelos.

O parsnip realiza um ótimo trabalho em unificar uma série de diferentes modelos estatísticos e de machine learning em um único ambiente. O pacote é extremamente conveniente porque permite que o usuário utilize uma única forma de se comunicar com diferentes modelos que inicialmente possuiam sintaxes totalmente diferentes ou exigiam dados em diferentes formatos (matrix, ts, data.frame).

Para utilizar o parsnip, sempre começamos definindo o modelo. Assim, para estimar uma regressão linear utilizamos a função linear_reg() e para estimar um random forest utilizamos a função rand_forest(). Contudo, muitos outros modelos estão presentes, como o modelo ARIMA (arima_reg), o modelo prophet (prophet_reg), Support Vector Machines (svm_poly e svm_rbf), regressão logística (logistic_reg), KNN (nearest_neighbor) e muitos outros. Uma lista completa de todos os modelos suportados pode ser encontrada na documentação do parsnip.

O pacote modeltime extende o total de modelos para incluir modelos exclusivos de séries temporais. Vamos utilizar ajustar os dados de log de gasolina para o modelo naïve e o modelo naïve sazonal. Primeiro vamos definir o modelo a ser ajustado com a função naive_reg(), e fixar o pacote R que contêm a função naive() original.

modelo_media <- window_reg() %>% 
  set_engine("window_function",
             window_function = mean)

modelo_snaive <- naive_reg(
        seasonal_period = 52
    ) %>%
    set_engine("snaive")

modelo_naive <- naive_reg() %>%
    set_engine("naive")

Para o modelo Naïve Sazonal, precisamos fixar o parâmetro de período da sazonalidade. Como os dados de gasolina estão em frequência semanal, temos uma sazonalidade bem peculiar, dado que o período de sazonalidade é de em média \(365,25/7=52,18\). A maioria dos modelos sazonais só aceitam valores inteiros para a frequência, e mesmo um valor aproximado de 52 períodos pode gerar resultados inadequados. Independemente dessa falha conhecida, vamos utilizar um seasonal_period = 52 como parâmetro do naive_reg.

6.3.5 Ajustando os modelos

Agora temos os três ingredientes mais importantes para nosso modelo preditivo: (1) temos as bases de treinamento e teste, (2) temos uma receita de bolo com o passo-a-passo do pré-processamento que deve ser aplicado em todas as bases de dados; e (3) declaramos o modelo que deve ser ajustado. Para facilitar a integração de todas essas peças, podemos utilizar o pacote workflows, parte da suite tidymodels.

Iniciamos um workflow sempre com a função workflow(). Adicionamos o modelo definido acima com add_model() e a receita que deve ser aplicada aos dados com add_recipe(). O último passo é o ajuste do modelo, onde passamos a base de treinamento construída pelo pacote rsample para estimar o modelo naïve e naïve sazonal.

workflow_media <- workflow() %>% 
  add_recipe(receita_gasolina) %>% 
  add_model(modelo_media) %>% 
  fit(training(gasoline_split))

## window_reg: Using window_size = Inf

workflow_naive <- workflow() %>% 
  add_recipe(receita_gasolina) %>% 
  add_model(modelo_naive) %>% 
  fit(training(gasoline_split))

workflow_snaive <- workflow() %>% 
  add_recipe(receita_gasolina) %>% 
  add_model(modelo_snaive) %>% 
  fit(training(gasoline_split))

Para facilitar o trabalho quando temos diversos modelos, podemos criar uma tabela de modelos com a função modeltime_table(), parte do pacote modeltime. Nela incluimos os arquivos com os modelos ajustados (workflow_*).

tbl_modelos <- modeltime_table(
  workflow_media,
  workflow_snaive,
  workflow_naive
  )

Por fim, usamos a função modeltime_calibrate() para produzir os valores previstos (fitted) para o período de teste e o valor dos resíduos. Mais a frente vamos analisar melhor os resíduos, mas antes vamos observar como os dois modelos realizaram as previsões para a oferta de produtos de gasolina (figura 6.4). Para tanto usamos a função modeltime_forecast(), para preparar um data.frame com as previsões e os dados observados, e a função plot_modeltime_forecast() para produzir a visualização desejada.

tbl_calibracao <- tbl_modelos %>% 
  modeltime_calibrate(new_data = testing(gasoline_split))

tbl_calibracao %>% 
  modeltime_forecast(new_data = testing(gasoline_split),
                     actual_data = us_gasoline) %>% 
  plot_modeltime_forecast()

Figure 6.4: Previsão de métodos naïve para produtos de gasolina nos EUA

A última observação da base de treinamento foi na semana do dia 30 de março de 2009. Naquele dia, o log do total de barris foi de 9,024. O método naïve simplesmente reproduziu este valor para todo o período de teste. Por isso vemos uma reta verde. Já o método da média, reproduziu o valor médio de todo o período. É possível notar que a média não é um bom previsor desta série, uma vez que a série passou por mudanças importantes na sua tendência.

O modelo naïve com sazonalidade, apesar de sua simplicidade, é capaz de capturar o comportamento da série surpreendemente bem, uma vez que a série tem um comportamento sazonal bem marcante.

É importante reforçar, que os modelos acima são meramente métodos de benchmarking. Em uma situação real, outros modelos mais adequados seriam utilizados, a exemplo dos modelos que serão vistos na seção 7, ?? e 9.

6.4 Valores ajustados e resíduos

Cada observação na série temporal pode ser prevista usando todas as observações anteriores. Chamamos estas novas observações de valores ajustados (fitted values), e eles são denotados por \(\hat{y}_{t|t-1}\), ou simplesmente \(\hat{y}_t\).

Já os resíduos são a diferença entre os valores observados e os valores ajustados do modelo:

\[e_t = y_t - \hat{y}_t\] Se os dados foram transformados, é sempre útil olhar os resíduos na escala transformada. Resíduos na escala transformada são chamados de resíduos da inovação, e podemos denotar por \(w_t - \hat{w}_t\), dado que \(w_t = \log{y_t}\).

Podemos acessar os valores observados, previstos e os resíduos para os dois modelos ao observar a tabela de calibração gerada pela função modeltime_calibrate().

tbl_calibracao %>% 
  unnest(.calibration_data) %>% 
  head(10) 

## # A tibble: 10 × 8
##    .model_id .model     .model_desc     .type Week       .actual .pred…¹ .resi…²
##        <int> <list>     <chr>           <chr> <date>       <dbl>   <dbl>   <dbl>
##  1         1 <workflow> WINDOW FUNC [I… Test  2009-04-06    2.19    2.12  0.0704
##  2         1 <workflow> WINDOW FUNC [I… Test  2009-04-13    2.21    2.12  0.0917
##  3         1 <workflow> WINDOW FUNC [I… Test  2009-04-20    2.21    2.12  0.0933
##  4         1 <workflow> WINDOW FUNC [I… Test  2009-04-27    2.19    2.12  0.0681
##  5         1 <workflow> WINDOW FUNC [I… Test  2009-05-04    2.19    2.12  0.0667
##  6         1 <workflow> WINDOW FUNC [I… Test  2009-05-11    2.22    2.12  0.102 
##  7         1 <workflow> WINDOW FUNC [I… Test  2009-05-18    2.26    2.12  0.135 
##  8         1 <workflow> WINDOW FUNC [I… Test  2009-05-25    2.20    2.12  0.0789
##  9         1 <workflow> WINDOW FUNC [I… Test  2009-06-01    2.21    2.12  0.0922
## 10         1 <workflow> WINDOW FUNC [I… Test  2009-06-08    2.24    2.12  0.115 
## # … with abbreviated variable names ¹​.prediction, ²​.residuals

É sempre útil checar se um modelo capturou de modo adequado as informações dos dados. Para tanto podemos utilizar algumas ferramentas de diagnósticos de resíduos para verificar se:

1. os resíduos são não correlacionados. Se existe correlação entre os resíduos, então existe informação presente nos resíduos que deveria ter sido utilizada para computar as previsões.

2. Os resíduos devem ter média zero. Se a média é diferente de zero, então as previsões estão viesadas.

Qualquer previsão que não satisfaz estas propriedades pode ser melhorado. Contudo, isto não significa que um modelo que satisfaça essas condições seja um modelo que não possa ser melhorado. Assim, checar essas informações é uma forma de garantir que o método está utilizando toda a informação dispoível, mas não é uma boa forma de selecionar o método ideal a ser escolhido.

É útil (mas não necessário) que os resíduos também variância constante (a chamada homocedasticidade), e sejam normalmente distribuidos. Estas propriedades tornam os cálculos de intervalo de confiança mais precisos.

Vamos utilizar a tabela de calibração para plotar os resíduos do modelo naïve sazonal. A figura 6.5 mostra os resíduos da previsão de gasolina utilizando o método naïve sazonal.

tbl_calibracao %>% 
  unnest(.calibration_data) %>% 
  filter(.model_desc == "SNAIVE [52]") %>% 
  plot_time_series(Week, .residuals, .title = "Resíduos do Modelo Naïve Sazonal")

Figure 6.5: Resíduos do Modelo Naïve Sazonal

Os resíduos parecem ter média zero no início e fim do período de teste, mas entre os anos de 2011 e 2014, temos resíduos que não possuem média zero, o que pode ser o resultado de um comportamento diferente da média história que não está sendo capturado pelo modelo de previsão. Isto pode indicar que as previsões produzidas por este método possuem um viés. É a impressão que temos quando analisamos a figura 6.4). A previsão parece sempre superestimar o log da oferta de produtos de gasolina.

Podemos ainda produzir o histograma dos resíduos do método naïve sazonal para verificar se os resíduos possuem uma distribuição que se assemelhe a uma normal. A figura 6.6 parece indicar que os resíduos não são exatamente normais.

tbl_calibracao %>% 
  unnest(.calibration_data) %>% 
  filter(.model_desc == "SNAIVE [52]") %>% 
  ggplot(aes(x = .residuals)) +
  geom_histogram() + 
  labs(title = "Histograma dos Resíduos de um método Naïve")

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.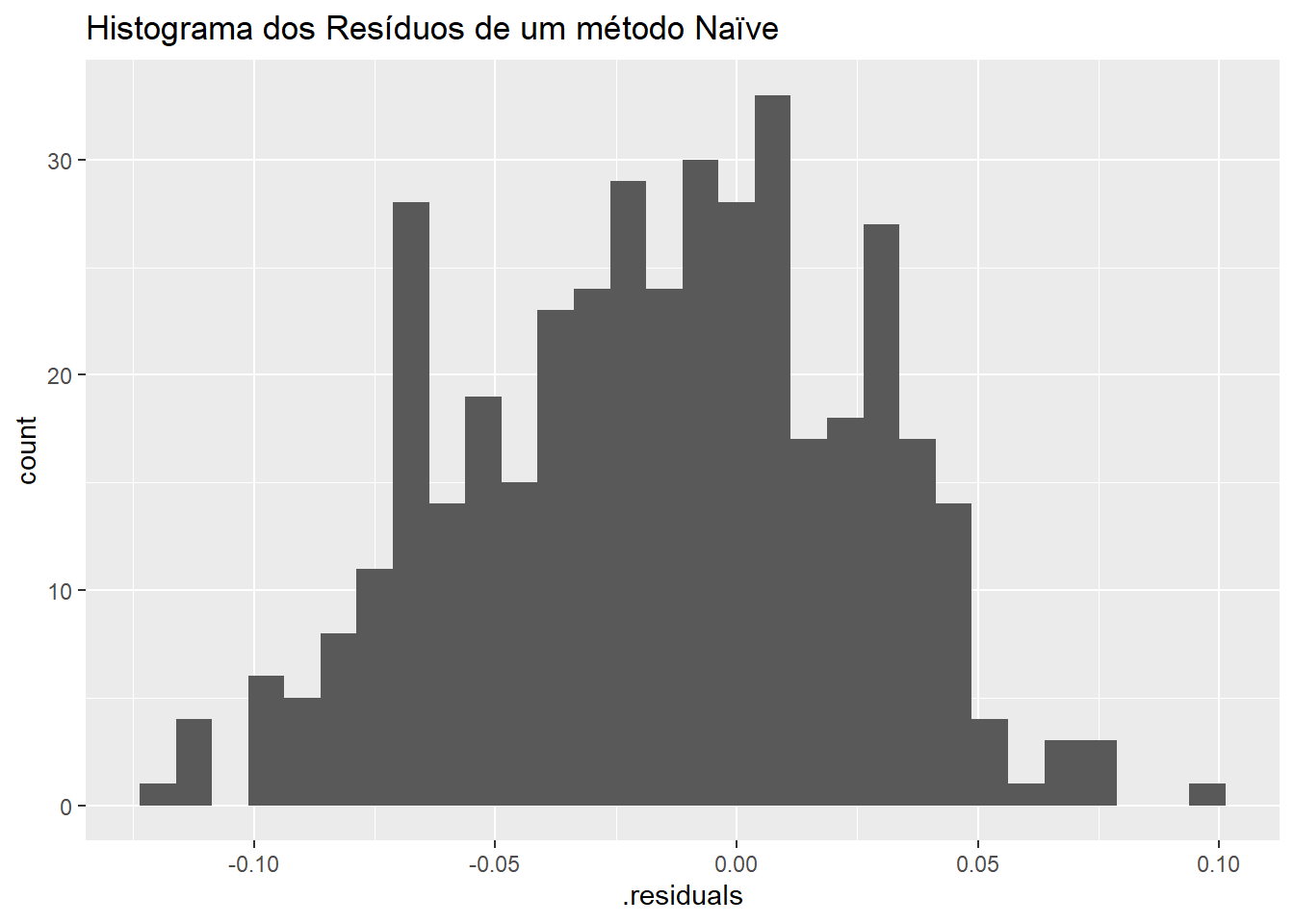

Figure 6.6: Histograma dos Resíduos de um método Naïve

Resíduos não normais podem indicar que as previsões a partir deste método podem até produzir resultados não viesados, mas os intervalos de confiança estimados podem ser imprecisos, uma vez que o seu cálculo assumem sempre distribuição normal.

Por fim, podemos verificar se os erros são autocorrelacionados utilizando a função de autocorrelação apresentada na seção xxx. A figura 6.7 mostra o correlograma produzido pela função plog_acf_diagnostics().

tbl_calibracao %>% 
  unnest(.calibration_data) %>% 
  filter(.model_desc == "SNAIVE [52]") %>% 
  plot_acf_diagnostics(Week, .residuals, 
                       .show_white_noise_bars = T,
                       .lags = 100,
                       .title = "Correlograma dos resíduos do método naïve aplicado a série de gasolina")

Figure 6.7: Correlograma dos resíduos do método naïve aplicado a série de gasolina

O correlograma parece indicar que os resíduos produzidos pelo método naïve são autocorrelacionados e que o modelo pode ser melhorado. A autocorrelação dos resíduos pode ser testada formalmente a partir de alguns testes estatísticos como o teste de Ljung-Box e o teste de Box-Pierce.

6.4.1 Teste de Ljung-Box

O gráfico da Função de Autocorrelação \(r_k\) mostra a autocorrelação para cada lag \(k\), e realiza um teste de hipótese que avalia se a autocorrelação \(r_k\) é estatísticamente diferente daquilo que se considera um ruido branco. Cada uma destes testes de hipótese carrega a possibilidade de produzir falsos positivos, de modo que alguns valores de autocorrelações moderados, podem ser confundidos com um resíduo com autocorrelação remanescente, mas quando tomamos em conjunto parecem excessivos. Assim, é possível testar se os primeiros \(K\) autocorrelações são significativamente diferentes de um ruído branco.

Um teste para um grupo de autocorrelações foi proposto por Box and Pierce (1970). Este teste é baseado na estatística

\[Q = n(\hat{r}^2_1 + \hat{r}^2_2 + ... + \hat{r}^2_K)\]

onde \(K\) é o número máximo de lags sendo considerados e \(n\) é o número de observações. Se cada \(r_k\) é próxima de zero, então \(Q\) será pequeno. Se alguns dos valores de \(r_k\) são grandes, então \(Q\) será grande. Hyndman and Athanasopoulos (2018) sugere um valor de \(K=10\) para dados não-sazonais, e de \(K=2m\), para dados sazonais, onde \(m\) é o período de sazonalidade.

Para um valor elevado de \(n\), \(Q\) tem uma distribuição chi-quadrado, mas segundo Ljung and Box (1978), mesmo valores de \(n = 100\) pode produzir aproximações não satisfatórias. Eles propõem uma versão modificada do teste de Box-Pierce, chamada de teste Ljung-Box, que define uma estatística de teste cuja distribuição nula é muito mais próxima da distribuição chi-quadrado. A estatística é dada por

\[Q_* = n(n+2)\left( \frac{\hat{r}^2_1}{n-1} + \frac{\hat{r}^2_2}{n-2} + ... + \frac{\hat{r}^2_K}{n-K} \right)\]

Novamente, valores elevados de \(Q_*\) sugerem que a autocorrelação não é um produto de ruído branco.

6.4.2 Função para Teste dos Resíduos

A função modeltime_residuals_test() toma os resíduos de cada modelo guardado na tabela de calibração tbl_calibracao e retorna uma série de testes estatísticos para os resíduos. A tabela 6.1 mostra os resultados dos testes de resíduos produzidos por esta função.

tbl_calibracao %>% 
  modeltime_residuals() %>% 
  modeltime_residuals_test() %>% 
  knitr::kable(caption = "Testes estatísticos para os resíduos")

Table 6.1: Testes estatísticos para os resíduos

.model_id	.model_desc	shapiro_wilk	box_pierce	ljung_box	durbin_watson
1	WINDOW FUNC [INF]	0.0025252	0	0	0.1446149
2	SNAIVE [52]	0.0149333	0	0	0.6583350
3	NAIVE	0.0025252	0	0	0.5446369

Além dos p-valores dos testes de Pierce-Box e Ljung-Box para autocorrelação, que não rejeitam a presença de autocorrelação, a tabela ainda mostra o resultado para o teste de Durbin-Watson e o p-valor para o teste de Shapiro-Wilks.

O teste de Durbin-Watson também testa a hipótese de autocorrelação, e parece indicar a presença de autocorrelação positiva (valores entre 0 e <2). O teste de Shapiro-Wilks testa mais rigorosamente a hipótese de normalidade dos resíduos, com uma hipótese nula de que os resíduos são normalmente distribuidos. O teste funciona ao calcular a correlação entre os resíduos e os quantis normais. Quanto menor esta correlação, maior a evidência de normalidade. Analisando a tabela, ao nível de significância de 0,05, nossos resíduos não parecem ser normalmente distribuidos, confirmando nossa inspeção visual do histograma dos resíduos.

6.5 Medindo a performance da previsão

O erro de previsão é medido como a diferença entre o valor observado e o previsto e pode ser escrito como

\[e_{T+h} = y_{T+h} - \hat{y}_{T+h|T}\] onde os dados de treinamento são dados por \(\{y_1, y_2, ..., y_T\}\) e dados de teste são dados por \(\{y_{T+1}, y_{T+2},...\}\).

Lembrando que os erros de previsão são a diferença entre dados observados e previstos para o período de teste, enquanto resíduos são a diferença entre dados observados e ajustados no período de treinamento.

6.5.1 Erros dependentes da escala

Algumas medidas de erro de previsão são dependentes da escala dos dados, não sendo indicados para comparação entre previsões feitas para séries temporais em escalas diferentes.

As medidas de erro dependente de escala mais comuns são o Erro Médio Absoluto (MAE, em inglês) e o Raiz quadrada do Erro Quadrado Médio (RMSE, em inglês):

\[\text{MAE} = \text{média}(|e_t|)\] \[\text{RMSE} = \sqrt{\text{média}(e_t^2)}\]

6.5.2 Erros de porcentagem

Erros de porcentagem não dependem da escala da série temporal, sendo utilizando para comparar performance de previsão de séries temporais de escalas diferentes. A médida mais utilizada é o Erro percentual da Média Absoluta (MAPE, em inglês). Esta medida é dada pela fórmula

\[\text{MAPE} = \text{média}(|p_t|)\] onde \(p_t = 100 e_t / y_t\).

A principal desvantagem deste tipo de medida é apresentar valores infinitos quando o valor de \(y_t = 0\) e valores extremos quando \(y_t \rightarrow 0\). Este tipo de médida também é assimétrica, na medida que penaliza mais erros negativos em detrimento de erros positivos. Uma medida percentual alternativa é a MAPE simétrica ou sMAPE, que é definida como

\[\text{sMAPE} = \text{média} \left(200 \frac{|y_t - \hat{y}_t|}{y_t + \hat{y}_t}\right)\]

Contudo, se \(y_t\) e \(\hat{y}_t\) são próximos de zero, a medida também envolve uma fração com denominador próximo de zero.

6.5.3 Erros Escalados

Como uma alternativa aos erros de percentagem, Hyndman and Koehler (2006) propõem reescalar os erros baseados na medida de MAE dos dados de treinamento de um método de previsão simples.

Para uma série temporal sem sazonalidade, uma forma de definir o erro de escala utiliza uma previsão naïve:

\[q_j = \frac{e_j}{\frac{1}{T-1} \sum_{t=2}^T |y_t - y_{t-1}|}\] Como o numerador e o denominador envolvem valores que estão na escala dos dados originais, \(q_j\) é independente da escala dos dados.

• \(q_j < 1\): \(q_j\) é produzido por uma previsão melhor que a média de previsão um passo-a-frente do modelo naïve computado nos dados de treinamente.

• \(q_j > 1\) se a previsão é pior.

Para dados com sazonalidade, o erro escalado pode ser definido ao utilizar uma previsão naïve com sazonalidade.

\[q_j = \frac{e_j}{\frac{1}{T-m} \sum_{t=2}^T |y_t - y_{t-m}|}\] Assim, o Erro Escalado Médio Absoluto (Mean Absolute Scaled Error, MASE) é dado por

\[\text{MASE} = \text{média}(|q_j|)\]

Alternativamente podemos calcular o Root Mean Squared Scaled Error (RMSSE) como

\[\text{RMSSE} = \sqrt{\text{média}(q_j^2)}\]

6.5.4 Função para Medidas de Performance

O pacote yardstick facilita a criação de medidas de performance dos modelos estimados, produzindo as principais medidas de desempenho para problemas de regressão (RMSE, R-Quadrado e outros) e de classificação (matriz de confusão, precisão, acurácia e outros).

O pacote modeltime nos fornece a função modeltime_accuracy(), que permite utilizar as funções do yardstick para objetos do tipo workflow.

A tabela 6.2 mostra as medidas de desempenho de previsão para os três modelos estimados. Para tanto, passamos a tabela de calibração para a função modeltime_accuracy(). Esta função produz uma tabela dinâmica com as principais métricas de performance discriminadas para cada modelo.

tbl_calibracao %>%
  modeltime_accuracy(new_data = testing(gasoline_split)) %>% 
  #select(.model_desc, mape, rmse) %>% 
  kableExtra::kable(caption = "Medidas de Desempenho para Previsão Naïve e Naïve com Sazonalidade")

## Warning: There were 2 warnings in `dplyr::mutate()`.
## The first warning was:
## ℹ In argument: `.estimate = metric_fn(truth = .actual, estimate =
##   .prediction, na_rm = na_rm)`.
## Caused by warning:
## ! There was 1 warning in `dplyr::summarise()`.
## ℹ In argument: `.estimate = metric_fn(truth = .actual, estimate =
##   .prediction, na_rm = na_rm)`.
## Caused by warning:
## ! A correlation computation is required, but `estimate` is constant and has 0 standard deviation, resulting in a divide by 0 error. `NA` will be returned.
## ℹ Run ]8;;ide:run:dplyr::last_dplyr_warnings()dplyr::last_dplyr_warnings()]8;; to see the 1 remaining warning.

Table 6.2: Medidas de Desempenho para Previsão Naïve e Naïve com Sazonalidade

.model_id	.model_desc	.type	mae	mape	mase	smape	rmse	rsq
1	WINDOW FUNC [INF]	Test	0.0752375	3.397220	3.086179	3.470716	0.0848558	NA
2	SNAIVE [52]	Test	0.0345147	1.585994	1.415764	1.573491	0.0431112	0.1741282
3	NAIVE	Test	0.0345067	1.582057	1.415437	1.574987	0.0437255	NA

Considerando que estamos comparando modelos diferentes aplicados aos mesmos dados, a questão de escala não é relevante. Da mesma forma, independentemente da medida utilizada, os dois modelos Naive parecem produzir resultados semelhantes, com o modelo de médias bem atrás.

6.6 Métodos de Reamostragem

Métodos de reamostragem são sistemas de simulação empírica que emulam o processo de usar parte dos dados para modelagem e uma parte diferente dos dados para avaliação da performance. O diagrama abaixo ilustra como métodos de reamostragem geralmente operam:

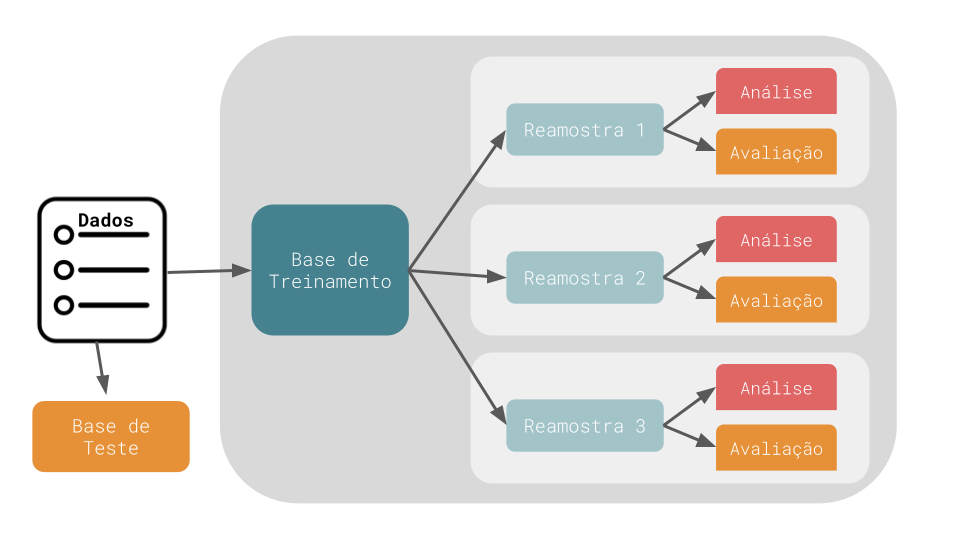
Métodos de Reamostragem

A reamostragem é conduzida apenas na base de treinamento. Para cada reamostragem, os dados são particionados em duas subamostras: uma base de análise, onde o modelo é ajustado e uma base de avaliação, onde o modelo é avaliado. Estas duas bases são análogas ao conjunto de treinamento e de teste. Utilizamos os termos análise e avaliação para evitar confusões com a divisão inicial entre base de treinamento e de teste.

Um dos métodos mais conhecidos de reamostragem é a validação cruzada. Neste tipo de reamostragem, os dados são aleatoriamente particionados em \(V\) conjuntos de tamanho igual (chamados de “folds”). Para \(V = 3\) e 1200 observações, podemos atribuir 300 observações para a base de teste e 900 para a base de treinamento. Podemos então selecionar aleatoriamente 300 observações para o conjunto de reamostragem 1, 300 para o conjunto de reamostragem 2 e 300 observações para o conjunto de reamostragem 3.

Para um processo de validação cruzada de 3-folds, para cada interação, um fold é guardado para gerar a avaliação do modelo e os outros dois folds são utilizados para ajustar o modelo. Este modelo continua para cada fold, para que sejam produzidos três conjuntos de medidas de performance. A medida final de performance é a média (ou mediana) das medidas das \(V\) replicações.

6.6.1 Validação Cruzada para Séries Temporais

Para dados de séries temporais, onde existem componentes como tendência e sazonalidade que dependem da ordem das observações, métodos de reamostragem como cross-validation e bootstrap podem impedir os modelos de estimar estas características.

Uma forma de corrigir este problema é utilizar validação cruzada para séries temporais. O diagrama abaixo mostra a base de treinamento de uma série temporal com 15 observações ordenadas no tempo. A primeira reamostragem possui 11 destas observações, sendo as 8 primeiras amostras reservadas para o périodo de análise e as 3 observações seguintes para o período de avaliação. Na segunda interação (reamostragem 2), a primeira amostra da base de treinamento é descartada e as bases de análise e avaliação “caminham” um período para frente.

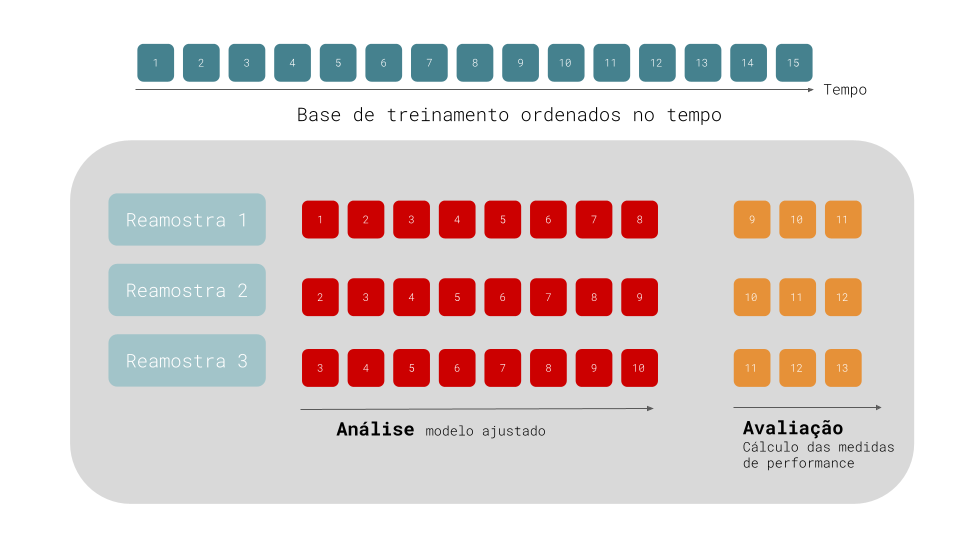
Validação Cruzada Para Séries Temporais

Algumas variações deste método existem: (1) podemos permitir que o conjunto de análise cresça cumulativamente (sem descartar as observações iniciais) e (2) podemos separar as diferentes reamostragens por blocos de semanas ou meses.

6.6.2 Implementando Validação Cruzada

O pacote timetk oferece a função time_series_cv para construção de validação cruzada para séries temporais. Além dos dados, a função toma uma série de diferentes parâmetros:

• initial: número de observações utilizados no período de análise.

• assess: número de observações utilizadas no período de avaliação.

• skip: permite que nem todos as observações sejam utilizadas na base de análise. Para dados diários, um skip=7 faz com que tenhamos apenas 1 informação por semana.

• lag: Incluir uma defasagem entre o período de análise e de avaliação.

• cumulative: Se o período de análise deve crescer cumulativamente.

• slice_limit: o número máximo de reamostragens a serem retornadas pela função.

Abaixo mostramos um exemplo de timee_series_cv com os dados de gasolina. Como temos 26 anos de dados semanais, vamos fixar o período de análise em 18 anos (initial = "18 years"), e o período de avaliação em 4 anos (assess = "4 years").

cross_validation <- time_series_cv(
  data = us_gasoline,
  date_var = Week,
  initial = "18 years",
  assess = "4 years",
  cumulative = TRUE
)

Este plano de validação cruzada produziu 104 conjuntos de treinamento de tamanho crescente. A figura 6.8 mostra o gráfico da validação cruzada para quatro destes grupos (slice 1, 20, 30 e 40). Usamos a função tk_time_series_cv_plan() para tornar o objeto cross_validation um data.frame, e plot_time_series_cv_plan() para gerar a visualização.

cross_validation %>%
  tk_time_series_cv_plan() %>%
  filter(.id %in% c("Slice001", "Slice040", "Slice070", "Slice104")) %>% 
  plot_time_series_cv_plan(Week, Barrels, .facet_ncol = 2, .interactive = FALSE)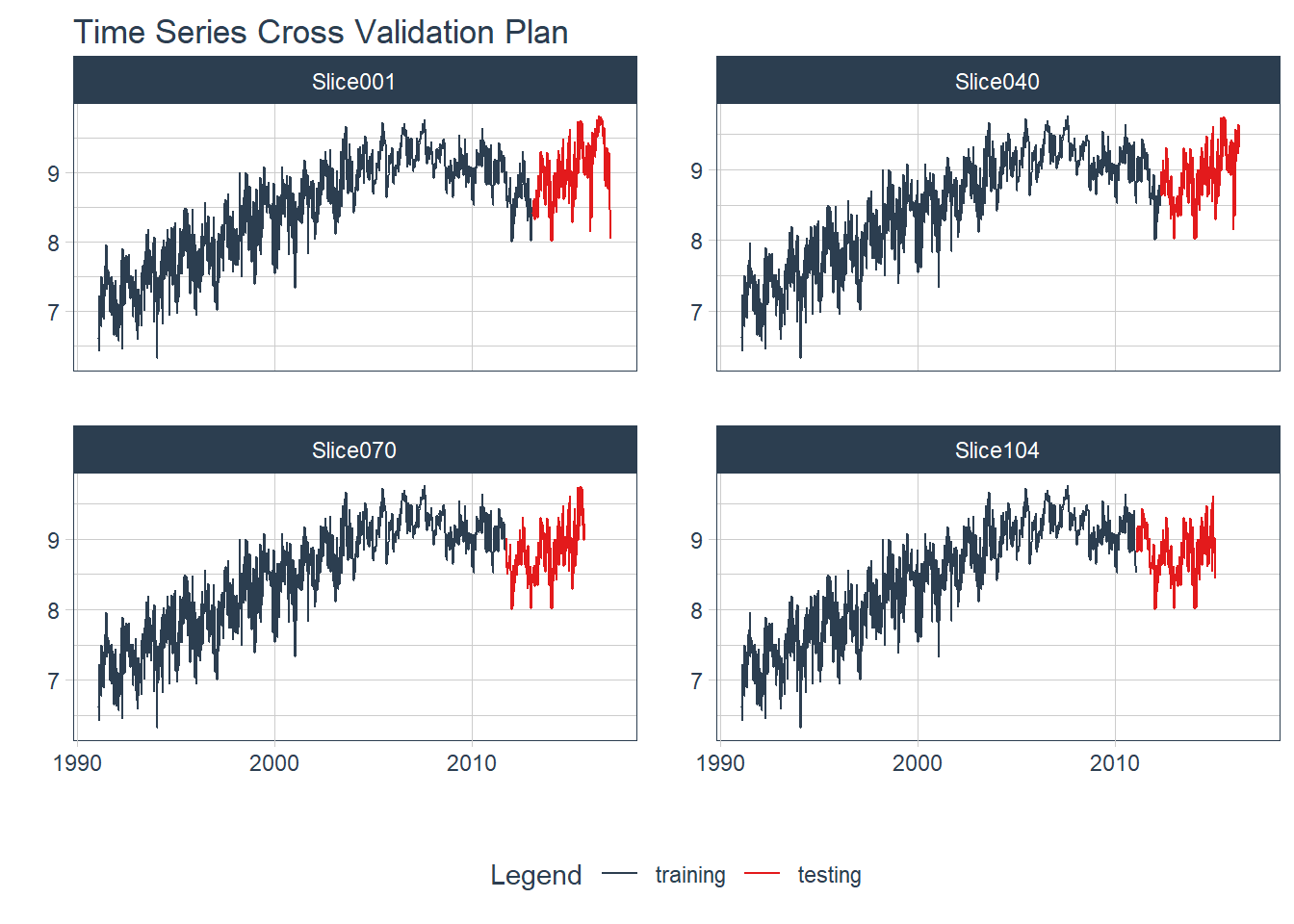

Figure 6.8: Validação Cruzada para Séries Temporais

6.6.3 Ajustando Modelos com Reamostragem

O pacote modeltime.resample fornece a função modeltime_fit_resamples para ajustar modelos contidos em uma tabela de modelos (tbl_modelos) para todas as reamostragens contidas no objetivo criado com time_series_cv(). Vamos ajustar o modelo naïve e naïve sazonal para cada um dos 104 folds.

library(modeltime.resample)

parallel_start(8)

ajustes_reamostragens <- tbl_modelos %>%
  modeltime_fit_resamples(
    resamples = cross_validation
  )

Rodar tantos modelos pode levar um longo tempo. Rodar os modelos em paralelo reduz substancialmente o tempo de execução e pode ser possível com o uso de funções como parallel_start(). Para ler mais, visite a documentação da função.

Após um tempo, o objeto ajustes_reamostragens terá informações de performance para os 208 modelos que foram ajustados. Na figura 6.9 temos uma visualizar da performance de cada reamostragem produzida pela função plot_modeltime_resamples(). Como temos 208 modelos ajustados, o gráfico se torna um pouco poluido.

ajustes_reamostragens %>%
  plot_modeltime_resamples(
    .point_size  = 1,
    .point_alpha = 0.8,
    .interactive = FALSE,
    .legend_show = F
  )

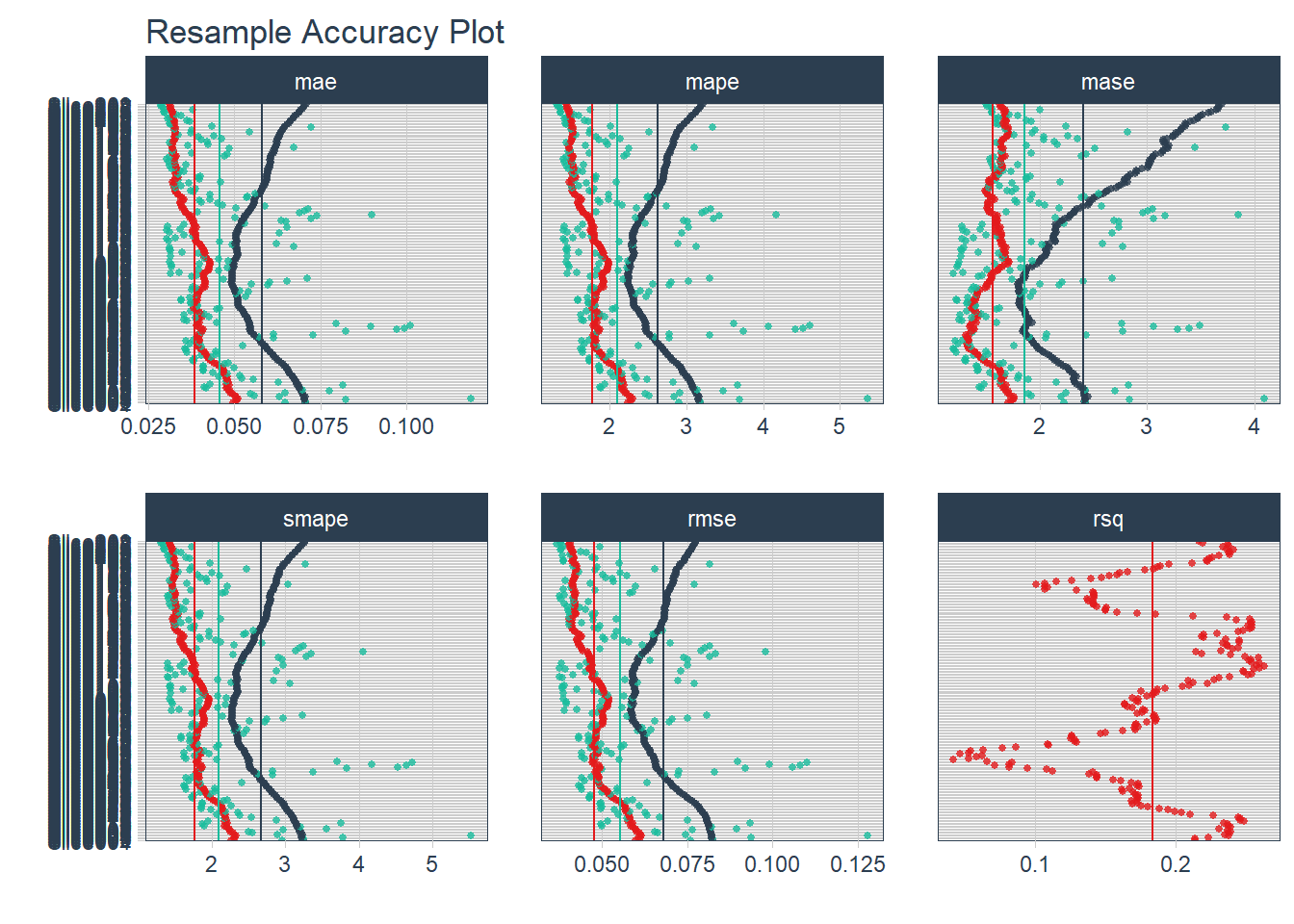
Figure 6.9: Gráfico de Medidas de Reamostragem

Uma visualização melhor das informações pode ser obtida ao se calcular a média (ou mediana) das medidas de performance dos 104 folds. Com a função modeltime_resample_accuracy() podemos calcular a média ou mediana das medidas de performance dos 208 modelos. Com table_modeltime_accuracy() podemos exibir estas informações de modo bastante conveniente.

ajustes_reamostragens %>%
  modeltime_resample_accuracy(summary_fns = mean) %>%
  table_modeltime_accuracy()

Analisando os resultados, e considerando que a quantidade de barris de gasolina podem ser iguais a zero, podemos utilizar o MAPE como critério de escolha. Neste caso, o método Naïve com Sazonalidade parece produzir previsões mais precisas.

References

Box, George EP, and David A Pierce. 1970. “Distribution of Residual Autocorrelations in Autoregressive-Integrated Moving Average Time Series Models.” Journal of the American Statistical Association 65 (332): 1509–26.

Hyndman, Rob J, and George Athanasopoulos. 2018. Forecasting: Principles and Practice. OTexts.

Hyndman, Rob J, and Anne B Koehler. 2006. “Another Look at Measures of Forecast Accuracy.” International Journal of Forecasting 22 (4): 679–88.

Ljung, Greta M, and George EP Box. 1978. “On a Measure of Lack of Fit in Time Series Models.” Biometrika 65 (2): 297–303.