Capítulo 5 Conceitos Teóricos
Aqui vamos descrever alguns conceitos fundamentais sobre a teoria de séries temporais. Em particular, entender o que é um processo estocástico, a média, a função de covariância, processos estocásticos e a função de autocorrelação.
5.1 Média, Variâncias e Covariâncias
Agora vamos introduzir várias medidas teoricas utilizadas para descrever como séries temporais se comportam. Como é usual em estatística, a descrição completa da série envolve uma função de distribuição multivariada a amostra conjunta dos valores \(y_1, y_2, ..., y_n\), enquanto que uma descrição mais econômica pode ser obtida em termos das funções média e de autocorrelação. Como a correlação é uma característica essencial da análise de séries temporais, as medidas de descrição mais úteis são aquelas expressadas em termos função de autocorrelação e função de autovariância.
Vamos discutir alguns conceitos importantes relacionados a todos os tipo de modelos estatísticos de série temporal. Especificamente podemos utilizar algumas medidas para descrever uma série temporal.
5.2 Função Média
A função média descreve o valor esperado de uma série temporal. Assim, para um processo estocástico \(\{ Y_t\}\), a função média é definida como:
\[\mu_t = E(Y_t)\] para \(t = 0,1,2,...\). Assim, \(\mu_t\) é o valor esperado do processo no tempo \(t\).
Exemplo 1: Função Média de Média Móvel
Para uma media móvel dada por \(\frac{1}{3}(w_{t-1} + w_t + w_{t+1})\), seu valor esperado (função média) é igual a zero, \(\mu_y = 0\). Assim, a função média ao redor de zero descreve bem o comportamento geral da média móvel. O mesmo pode ser dito do ruído branco.
df %>%
ggplot(aes(x = x, y = ruido_branco)) +
geom_line(aes(color = "Ruído Branco")) +
geom_hline(aes(yintercept = 0, color = "Função Média"), linetype = 2, size = 1.5) +
labs(x = "Tempo", y = "",
title = "Média Móvel",
subtitle = "Função Média da Média Móvel é Zero",
color = "") +
theme(legend.position = "bottom")## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.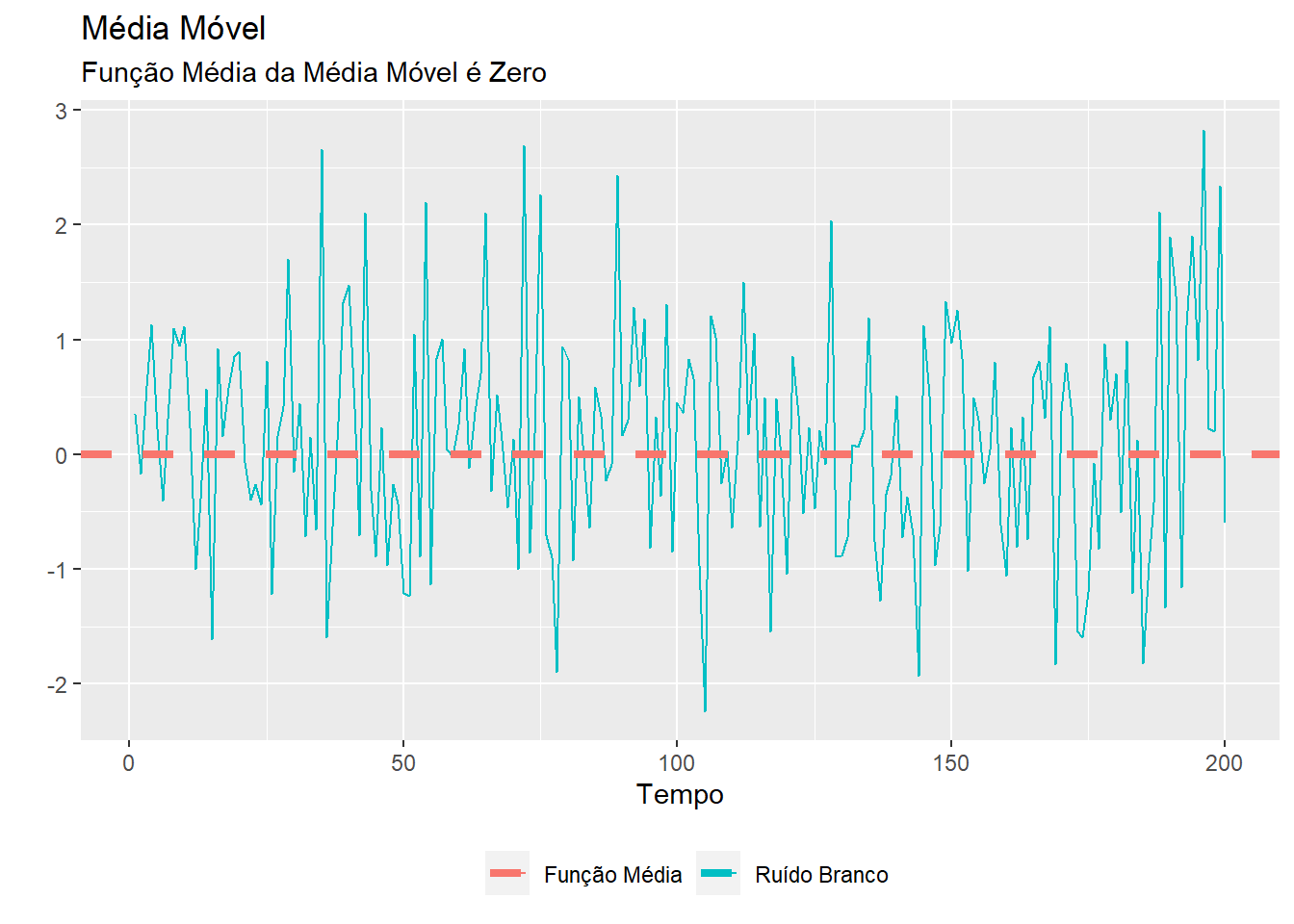
(#fig:ruido_media)Função Média de um ruído branco
Exemplo 2: Função Média de Random Walk com Drift
Para um random walk com drift qual a função média? Dado que este modelo é dado por \(y_t = \delta t + \sum_{j=1}^t w_t\), como \(E(w_t) = 0\) e como \(\delta\) é uma constante, temos
\[\mu(yt) = \delta t\]
Assim, a função média de uma random walk com drift é uma linha reta com inclinação \(\delta\). Uma comparação de uma random walk com drift e sua função média pode ser vista na figura 5.1.
df %>%
# criar a função média da random walk
mutate(funcao_media_random_walk = .2*x) %>%
ggplot(aes(x = x)) +
geom_line(aes(y = random_walk_drift, color = "Random Walk com Drift")) +
geom_line(aes(y = funcao_media_random_walk, color = "Função Média"), linetype = 2, size = 1.5) +
labs(x = "Tempo", y = "",
title = "Random Walk com Drift Delta = 0.2",
subtitle = "A função Média é uma linha Reta com Inclinação Delta = 0.2",
color = "Modelo:")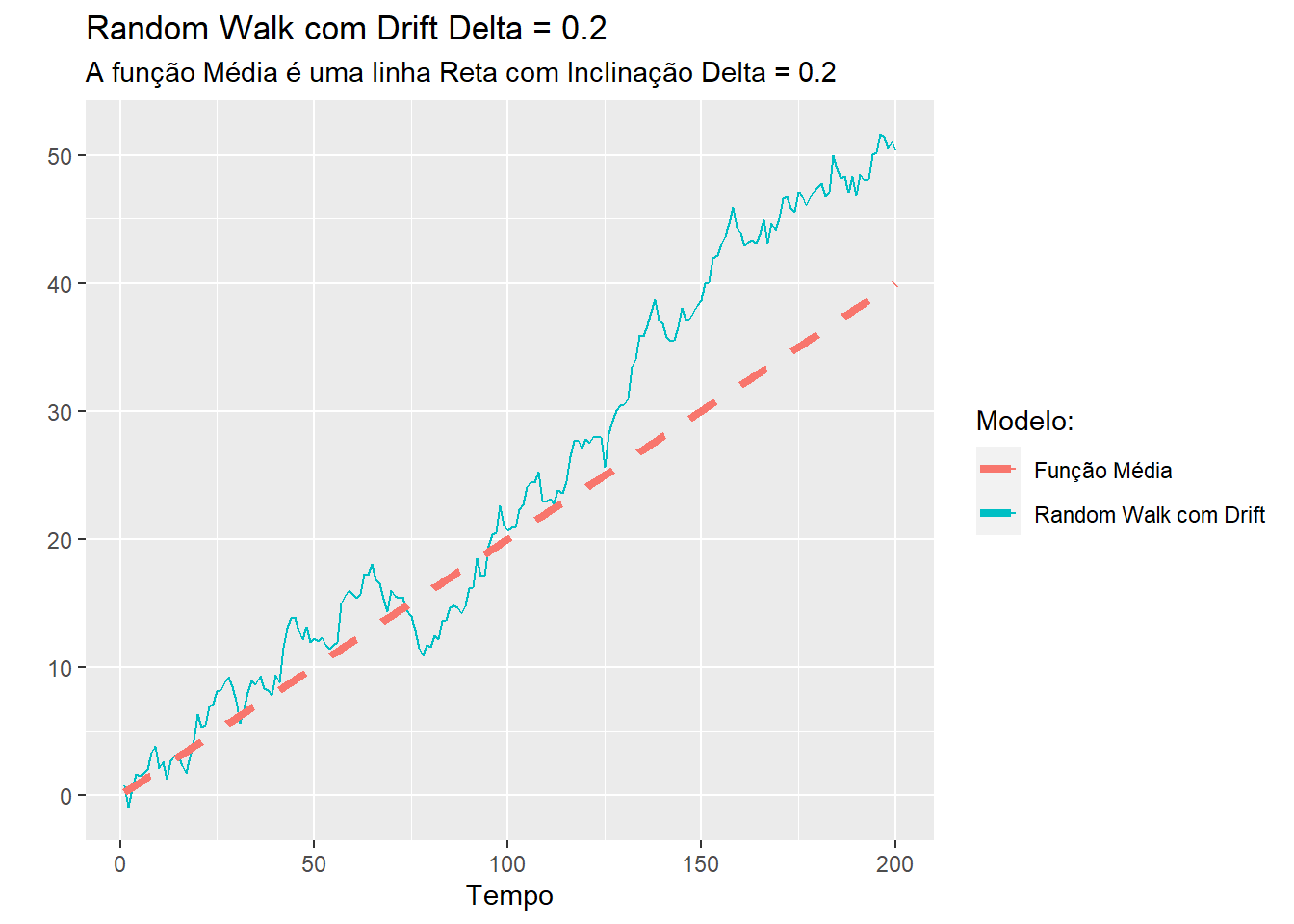
Figure 5.1: Função média de uma série random walk com drift
Exemplo 3: Função Média de um Sinal mais Ruído
A função média para um modelo aditivo na forma \(y_t = s_t + w_t\) é obtido por:
\[\mu_{yt} = E(y_t) = E[2 \cos(2\pi \frac{2t + 15}{50}) + w_t]\]
Novamente, \(E(w_t) = 0\) e os demais termos são constantes, logo:
\[\mu_{yt} = E(y_t) = 2 \cos(2\pi \frac{2t + 15}{50})\] A média móvel é apenas o sinal sem o ruído.
df %>%
ggplot(aes(x = x)) +
geom_line(aes(y = curva_onda, color = "Função Média"), size = 1.5, linetype = 2) +
geom_line(aes(y = curva_onda_ruido, color = "Sinal com Ruído")) +
labs(title = "Curva em Onda e Sua Função Média",
subtitle = "A função Média é o Sinal sem Ruído",
color = "") +
theme(legend.position = "bottom")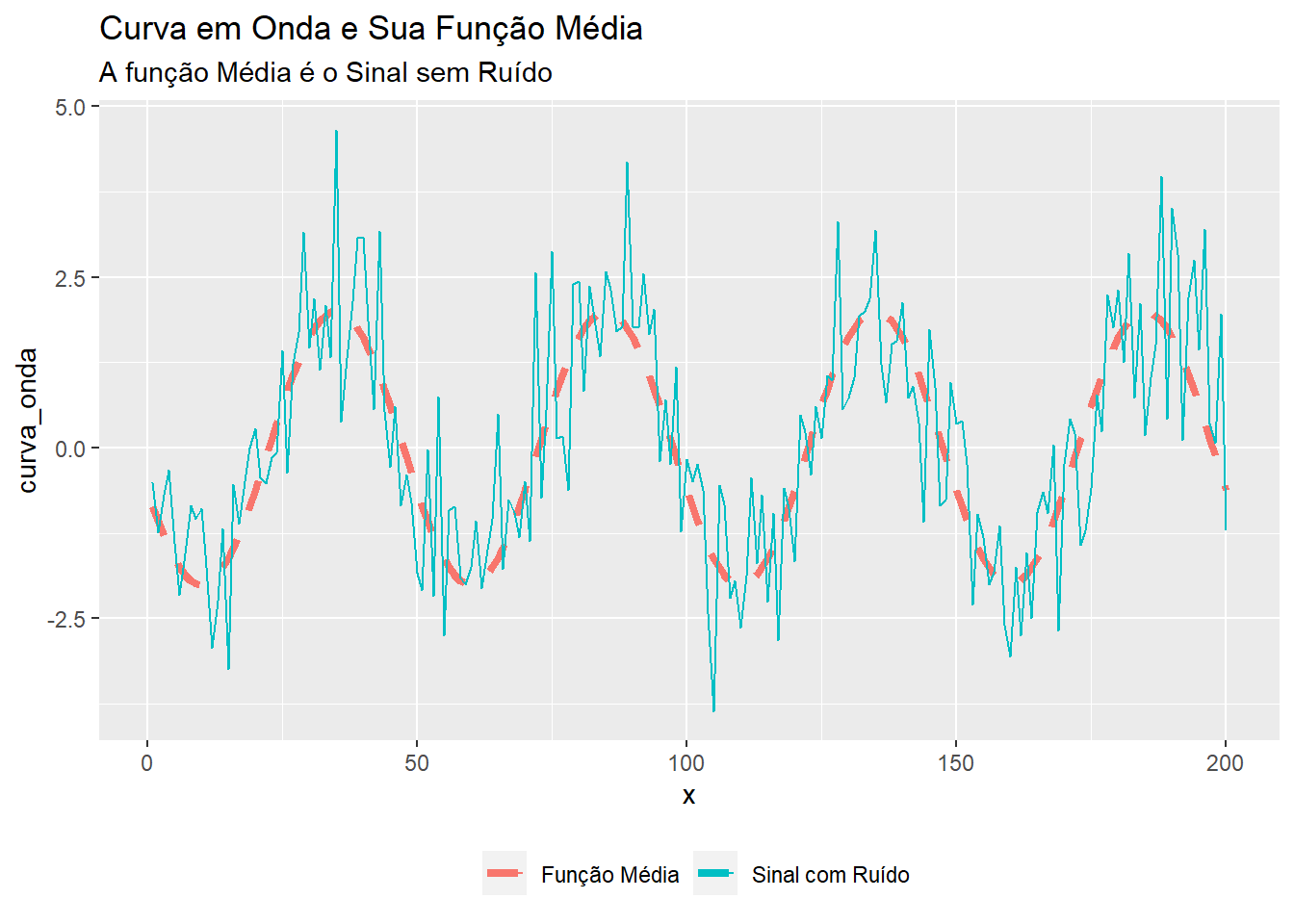
(#fig:sinal_media)Função Média de uma série com sinal
5.3 Função de Autocovariância
A função de autocovariância mostra a covariância de um processo consigo mesmo em dois pontos diferentes no tempo. Assim, para uma série mensal de preços, a função de autocovariância mostra a relação entre \(y_{jan}\) e \(y_{fev}\), que são os valores observados de preço para janeiro e fevereiro, respectivamente.
A função de autocovariância \(\gamma_{t,s}\) é definida como:
\[\gamma_{t,s} = Cov(Y_t, Y_s)\]
para \(t,s=0,1,2,...\)
Onde \(Cov(Y_t,Y_s) = E[(Y_t - \mu_t)(Y_s - \mu_s)] = E[Y_t Y_s) - \mu_t \mu_s\).
Portanto, a autocovariância mede a dependência linear entre dois pontos na mesma série observadas em pontos diferentes. Séries que são muito suavizadas exibem funções de autocovariância que permanecem altas mesmo quando o \(t\) e o \(s\) estão muito longes entre si. Séries com muita agitação tendem a ter funções de autocovariância que são próximas de zero para valores muito distantes entre si.
Lembre que se \(s = t\), ou seja, se estivermos comparando uma observação no tempo consigo mesmo, a autovariância se reduz ao valor de variância, porque
\[\gamma_{y}(t,t) = E[(y_t - \mu_t)^2] = \text{Var}(x_t)\]
Exemplo 1: Autocovariância de Ruído Branco
Para uma série temporal ruído branco \(w_t\) que tem \(E(w_t)=0\), temos que
\[\gamma_w = Cov(w_s, w_t) = 0\]
para \(s \neq t\). Assim, a relação linear entre duas observações é zero. O valor de uma observação num ponto no tempo não influencia em nada os valores observados nos demais pontos do tempo.
Exemplo 2: Autocovariância de uma Média Móvel
Considere nosso exemplo de uma média móvel. Assim,
\[\gamma_v (s,t) = cov(v_s, v_t) = cov \{ \frac{1}{3}(w_{s-1} + w_s + w_{s+1}), \frac{1}{3}(w_{t-1} + w_t + w_{t+1}) \}\]
Quando \(s = t\), temos
\[\gamma_v (s,t) = \frac{1}{9}cov\{(w_{t-1} + w_t + w_{t+1}), (w_{t-1} + w_t + w_{t+1}) \}\]
\[\gamma_v (s,t) = \frac{1}{9}\[ cov(w_{t-1}, w_{t-1} + cov(w_{t} + w_t) + cov(w_{t+1} + w_{t+1}) \]\]
\[\gamma_v (s,t) = \frac{3}{9} \sigma^2_w\]
O mesmo exercício pode ser feito para \(s = t + 1\), quando analisamos observações que estão distantes uma observação entre si (janeiro e março, por exemplo), onde \(\gamma_v (t + 1, t) = \frac{2}{9}\sigma^2_w\). Quando as observaçãos estão separadas por dois períodos, \(|s-t| = 2\), temos \(\gamma_v(s,t) = \frac{1}{9}\sigma^2_w\), e quando as observações estão separadas por mais de dois períodos, \(|s-t| > 2\), temos \(\gamma_v(s,t) = 0\).
Assim, quando suavizamos um ruído branco utilizando uma média móvel, adicionamos um pouco de covariância, mas esta dependência linear se reduz com o aumento da separação entre os valores. Assim, a relação entre janeiro e fevereiro é mais forte que a relação entre janeiro e março. Contudo, a relação entre janeiro e abril seria igual a zero, dado que \(| \text{Jan} - \text{Abr} | > 2\).
Exemplo 3: Autocovariância de um Random Walk
Para um modelo random walk, \(y_t = \sum_{j = 1}^t w_t\), temos que
\[\gamma_y (s,t) = cov(y_s, y_t) = cov \left( \sum_{j=1}^2 w_j, \sum_{k=1}^t w_t\right) = \min\{s,t\} \sigma^2_w\]
porque o \(w_t\) são variáveis não correlacionadas entre si. Nota que, diferentemente dos exemplos anteriores, a função autocovariância de uma random walk depende no valor em particular de \(s\) e \(t\), e não na separação entre as observações ou no lag. Perceba também que a variãncia de uma random walk, \(var(y_t) = t \sigma^2_w\), aumenta sem limites quando \(t\) cresce. O efeito desta variância pode ser observada na figura para o random walk. Conforme \(t\) aumenta, mais e mais a variável se distancia da sua função média \(\delta t\).
df %>%
# criar a função média da random walk
mutate(funcao_media_random_walk = .2*x) %>%
ggplot(aes(x = x)) +
geom_line(aes(y = random_walk_drift, color = "Random Walk com Drift")) +
geom_line(aes(y = funcao_media_random_walk, color = "Função Média"), linetype = 2, size = 1.5) +
labs(x = "Tempo", y = "",
title = "Random Walk com Drift Delta = 0.2",
subtitle = "Quanto maior o t, maior a distância entre a Série e sua Função Média",
color = "Modelo:") +
theme(legend.position = "bottom")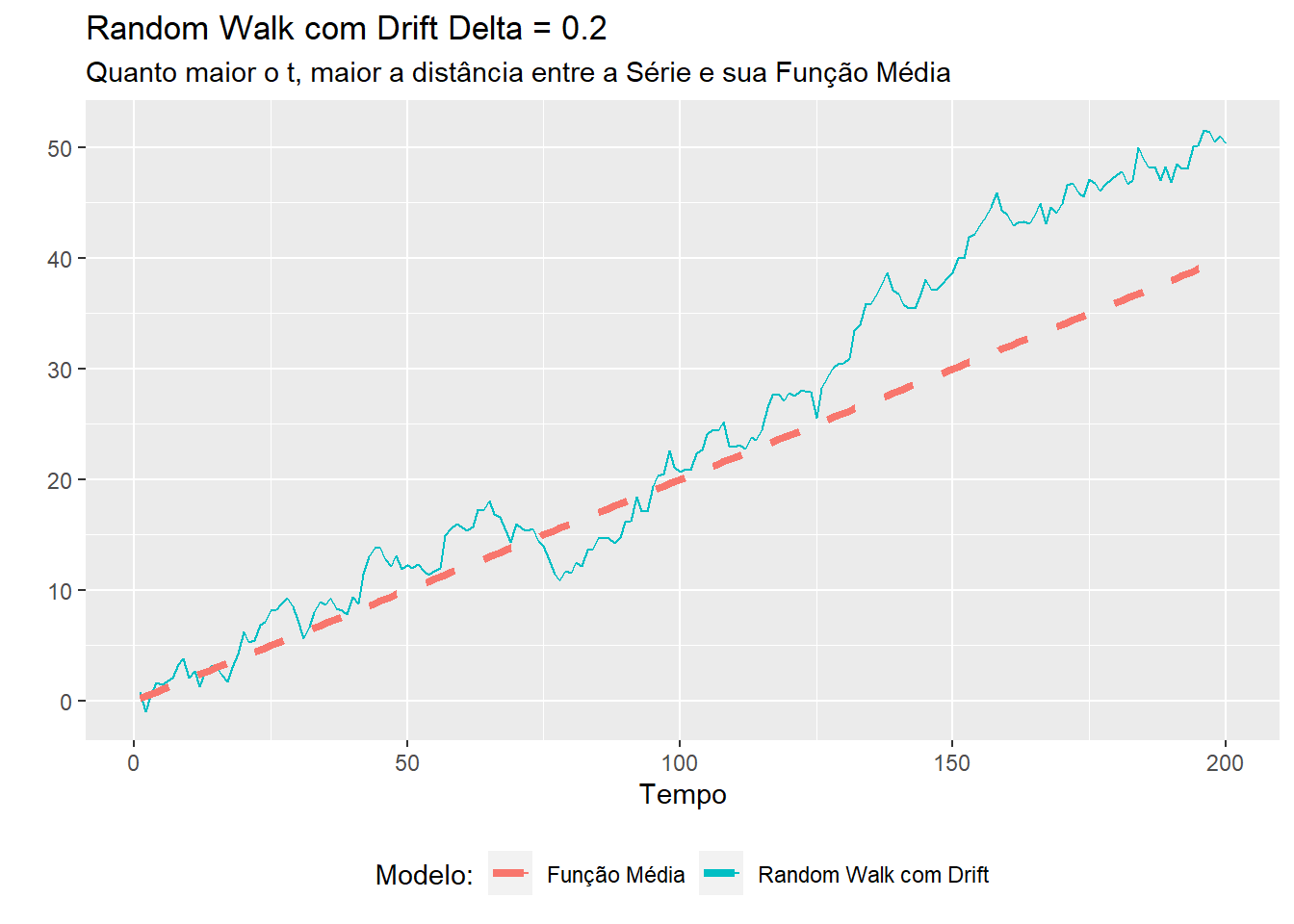
Figure 5.2: Autocovariância de uma random walk com drift
5.4 A Função de Autocorrelação (FAC)
A correlação mensura a relação linear entre duas variáveis. A autocorrelação por sua vez mede a relação linear entre valores defasados ( lagged ) de uma série temporal.
Uma forma de mensurar como um valor se relaciona a um valor passado é utilizando a Função de Autocorrelação (FAC), ou ACF em inglês. Ela mede a previsibilidade linear da série no tempo \(t\), usando apenas os valores de \(y_s\). A função de autocorrelação é definida como
\[\rho (s,t) = \frac{\gamma(s,t)}{\sqrt{\gamma(s,s)\gamma(t,t)}}\]
O valor de \(\rho\), a covariância, esta sempre no intervalo \([-1,1]\). Se pudermos prever \(y_t\) perfeitamente a partir de \(y_s\) através de uma relação linear \(y_t = \beta_0 + \beta_1 y_s\), então a correlação será \(+1\) quando \(\beta_1 > 0\), e a correlação será \(-1\) quando \(\beta_1 <0\). Portanto, temos uma medida grosseira da nossa habilidade de prever a série no tempo \(t\) utilizando os valores no tempo \(s\).
Vamos observar esse comportamento na prática utilizando os dados trimestrais de produção de cerveja. A figura 5.3 mostra a série.
beer2 <- window(ausbeer, start=1992)
autoplot(beer2) +
ggtitle("Produção trimestral de Cerveja, Australia") +
ylab("") + xlab("Ano")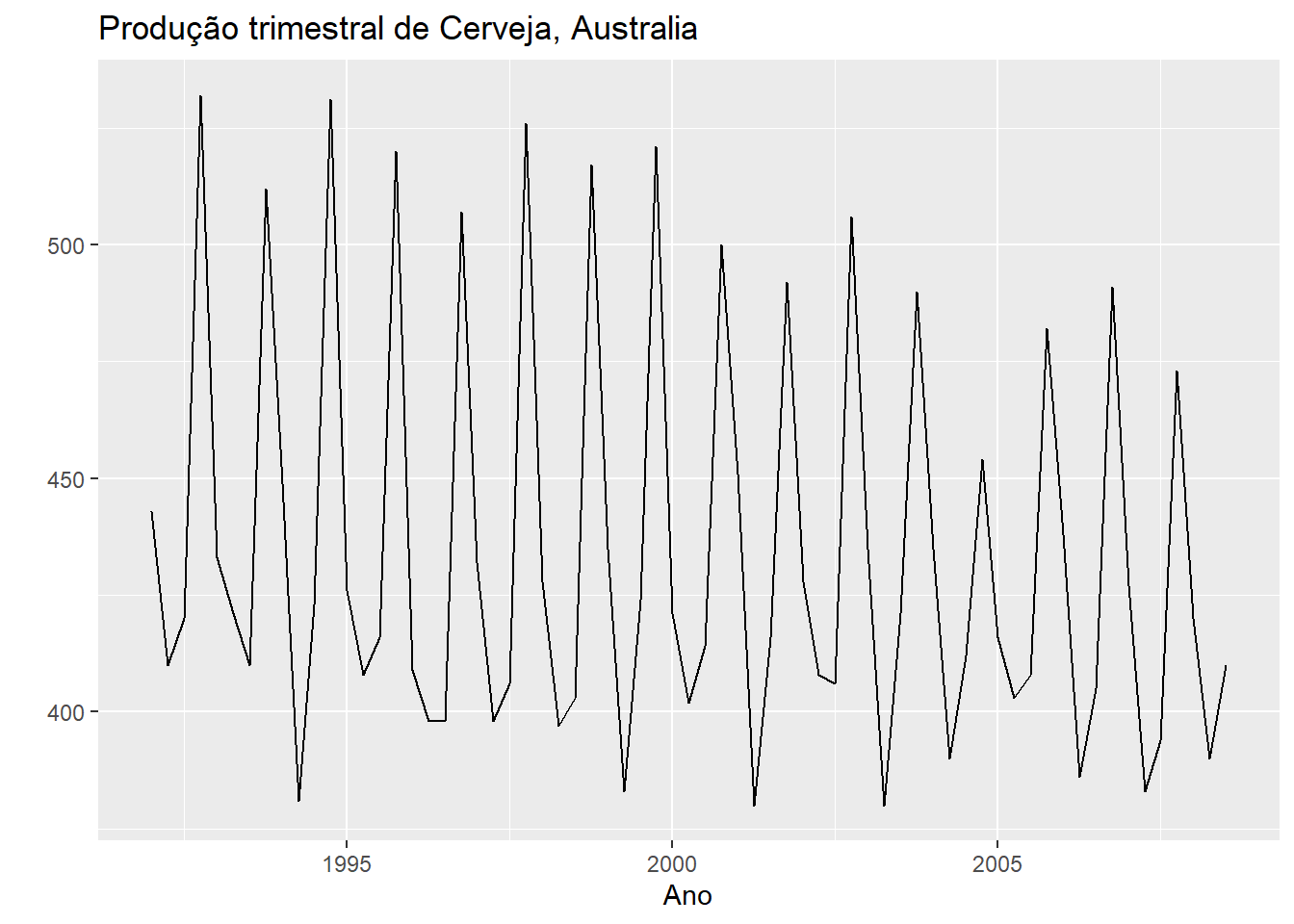
Figure 5.3: Produção trimestral de cerveja
É possível observar que os dados possuem um comportamento sazonal bem marcante. Vamos visualizar esse comportamento utilizando o correlograma, o gráfico que nos retorna os coeficientes de autocorrelação.
library(forecast)
ggAcf(beer2)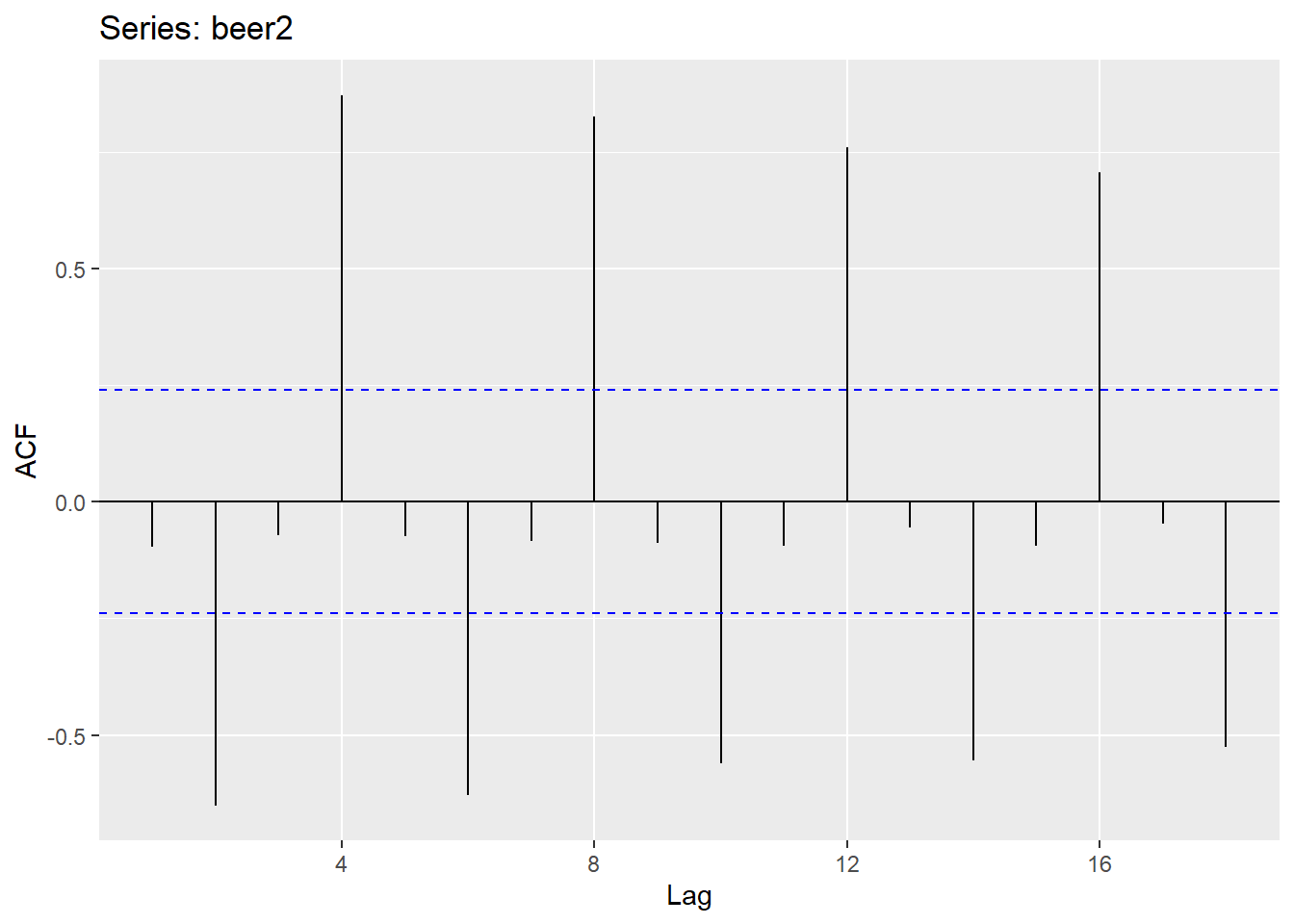
Figure 5.4: Função de autocorrelação para a produção trimestral de cerveja
O gráfico parece mostrar:
O \(r_4\) é maior que outros lags. Isso é um resultado do padrão sazonal da série. Os picos tendem a ser separados por quatro trimestres e os vales tendem a ser separados por quatro trimestres.
\(r_2\) é mais negativo que outros lags porque os vales e picos tendem a ser separados por dois trimestres.
A linha azul indica se a correlação é significamente diferente de zero.
5.4.1 Tendência e sazonalidade em Correlogramas
Quando os dados possuem uma tendência, as autocorrelações para pequenas defasagens é grande e positiva porque as observações próximas no tempo possuem valores semelhantes.
Assim, o ACF de uma série com tendência tende a ter valores positivos que lentamente decaem conforme o número de valores defasados (lags) aumenta.
A demanda por energia elétrica na australia (figura 5.5) possui um misto de padrão sazonal e tendência.
aelec <- window(elec, start=1980)
autoplot(aelec) + xlab("Year") + ylab("GWh")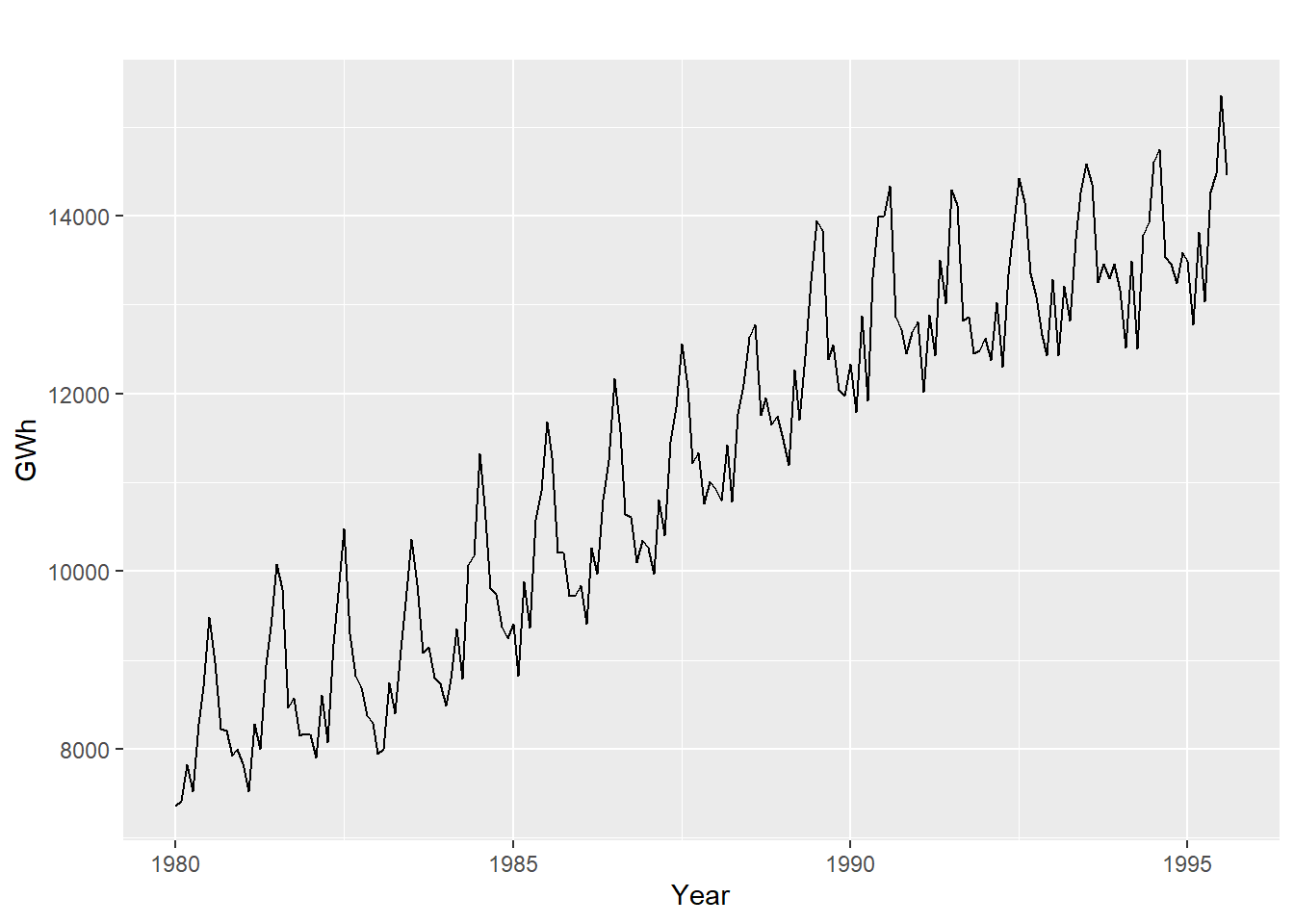
Figure 5.5: Demanda por Energia Elétrica na Australia, 1980-1995
E a função de autocorrelação da série (figura 5.6) tem um decaimento lento devido a tendência, enquanto possui pequenas ondas, que ocorrem devido ao comportamento sazonal da série.
ggAcf(aelec, lag=48)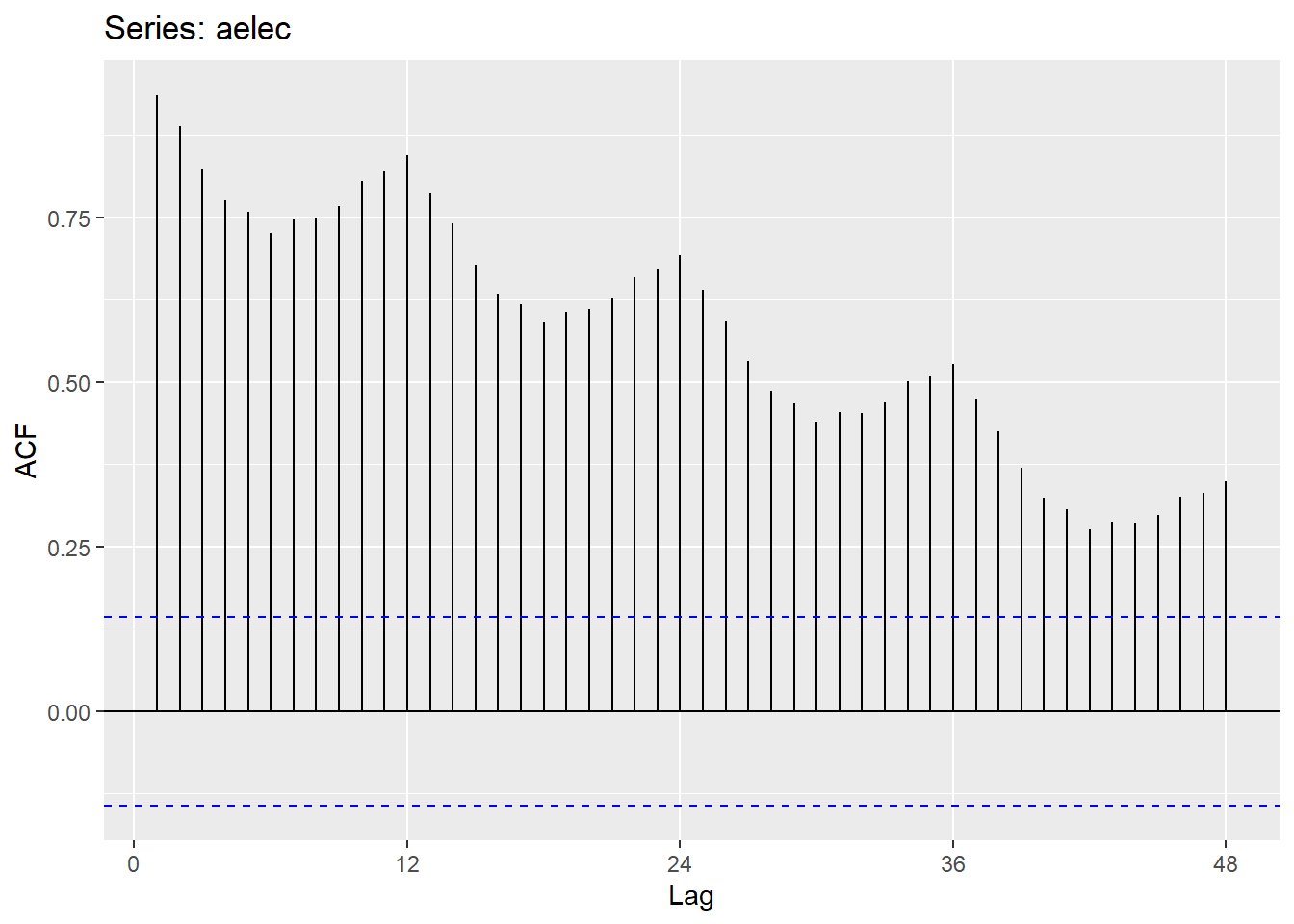
Figure 5.6: ACF da demanda australiana por energia elétrica
O pacote timetk fornece uma função para gerar o correlograma.
aelec_df <- data.frame(electrical_demand = matrix(aelec),
date = time(aelec)) %>%
mutate(date = as.Date(date))
aelec_df %>%
plot_acf_diagnostics(date, electrical_demand,
.show_white_noise_bars = T,
.interactive = F)## Max lag exceeds data available. Using max lag: 187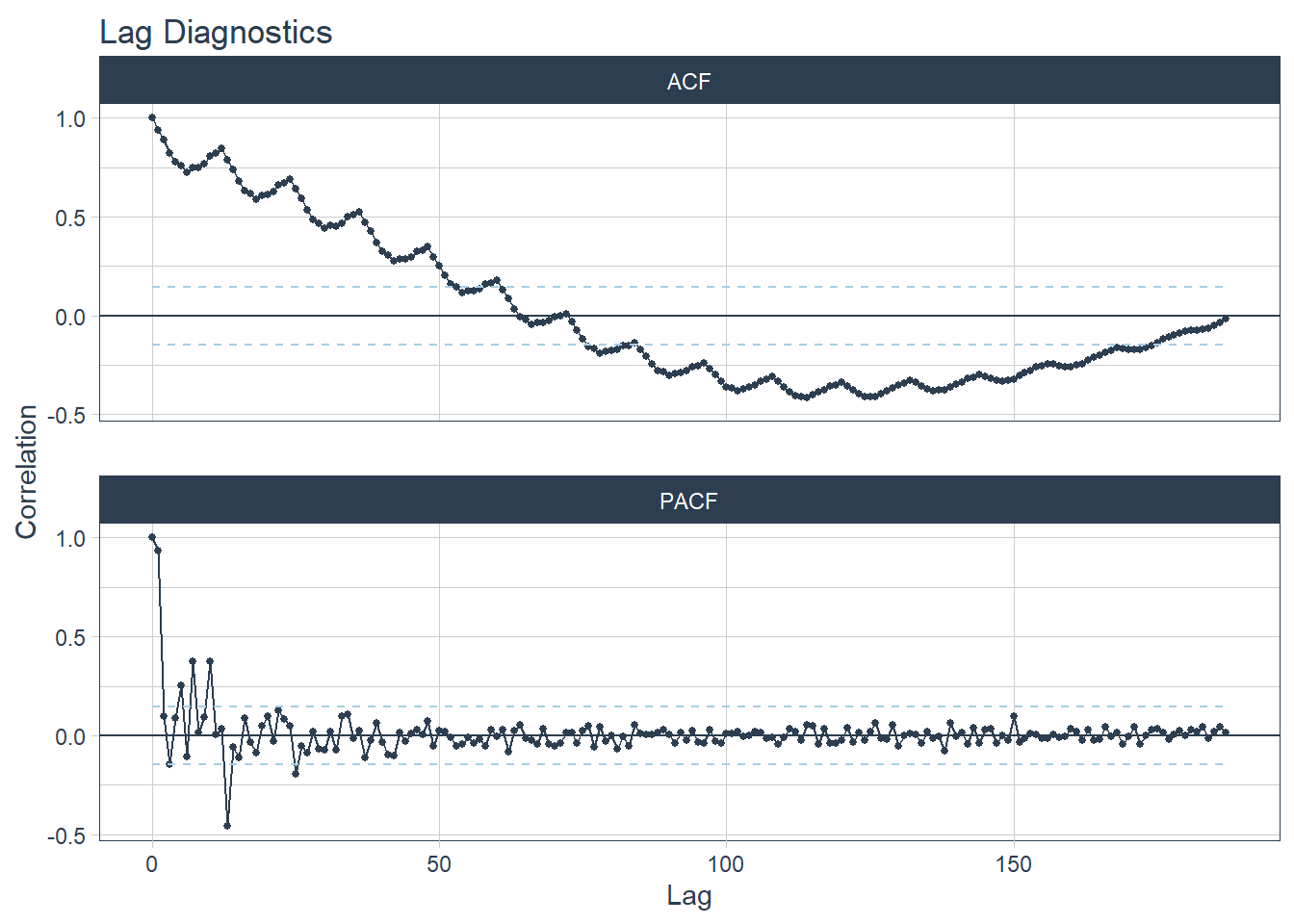
A figura ilustra além do ACF, a função de autocorrelação parcial (PACF, em inglês) que será melhor explicada na seção xxx.
5.4.2 A Função de Covariância-Cruzada e de Correlação-Cruzada
De maneira geral, gostariamos de medir a previsibilidade de uma outra série \(y_t\) a partir da série \(x_s\). Assumindo que ambas as séries tem variância finita, nós temos a seguinte definição para a função de covariância cruzada:
\[\gamma_{x,y}(s,t) = cov(x_s, y_t) = E[(x_s - \mu_{xs})]\]
A função de correlação cruzada (FCC) é dada por:
\[\rho_{xy}(s,t) = \frac{\gamma_{xt}(s,t)}{\sqrt{\gamma_{x}(s,s) \gamma_{y}(t,t)}}\]
Podemos inclusive extender a ideia acima para o caso de mais de duas séries.
O pacote timetk oferece um banco de dados de vendas semanais na rede walmart, com informações de vendas semanais para diferentes departamentos de lojas selecionadas da rede. O banco de dados ainda possui covariadas adicionais como isHoliday, que indica se a semana específica possui um feriado, Temperature, que indica a temperatura média da semana e Fuel_Price, que indica o preço do combustível naquela semana. Abaixo uma pequena amostra dos dados disponíveis:
walmart_sales_weekly %>%
head() %>%
knitr::kable(caption = "Vendas semanais das lojas walmart")| id | Store | Dept | Date | Weekly_Sales | IsHoliday | Type | Size | Temperature | Fuel_Price | MarkDown1 | MarkDown2 | MarkDown3 | MarkDown4 | MarkDown5 | CPI | Unemployment |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1_1 | 1 | 1 | 2010-02-05 | 24924.50 | FALSE | A | 151315 | 42.31 | 2.572 | NA | NA | NA | NA | NA | 211.0964 | 8.106 |
| 1_1 | 1 | 1 | 2010-02-12 | 46039.49 | TRUE | A | 151315 | 38.51 | 2.548 | NA | NA | NA | NA | NA | 211.2422 | 8.106 |
| 1_1 | 1 | 1 | 2010-02-19 | 41595.55 | FALSE | A | 151315 | 39.93 | 2.514 | NA | NA | NA | NA | NA | 211.2891 | 8.106 |
| 1_1 | 1 | 1 | 2010-02-26 | 19403.54 | FALSE | A | 151315 | 46.63 | 2.561 | NA | NA | NA | NA | NA | 211.3196 | 8.106 |
| 1_1 | 1 | 1 | 2010-03-05 | 21827.90 | FALSE | A | 151315 | 46.50 | 2.625 | NA | NA | NA | NA | NA | 211.3501 | 8.106 |
| 1_1 | 1 | 1 | 2010-03-12 | 21043.39 | FALSE | A | 151315 | 57.79 | 2.667 | NA | NA | NA | NA | NA | 211.3806 | 8.106 |
Na figura 5.7 exibimos a série de vendas no tempo apenas para o departamento 1 da loja 1.
walmart_sales_weekly %>%
filter(id == "1_1") %>%
plot_time_series(Date, Weekly_Sales, .interactive = F)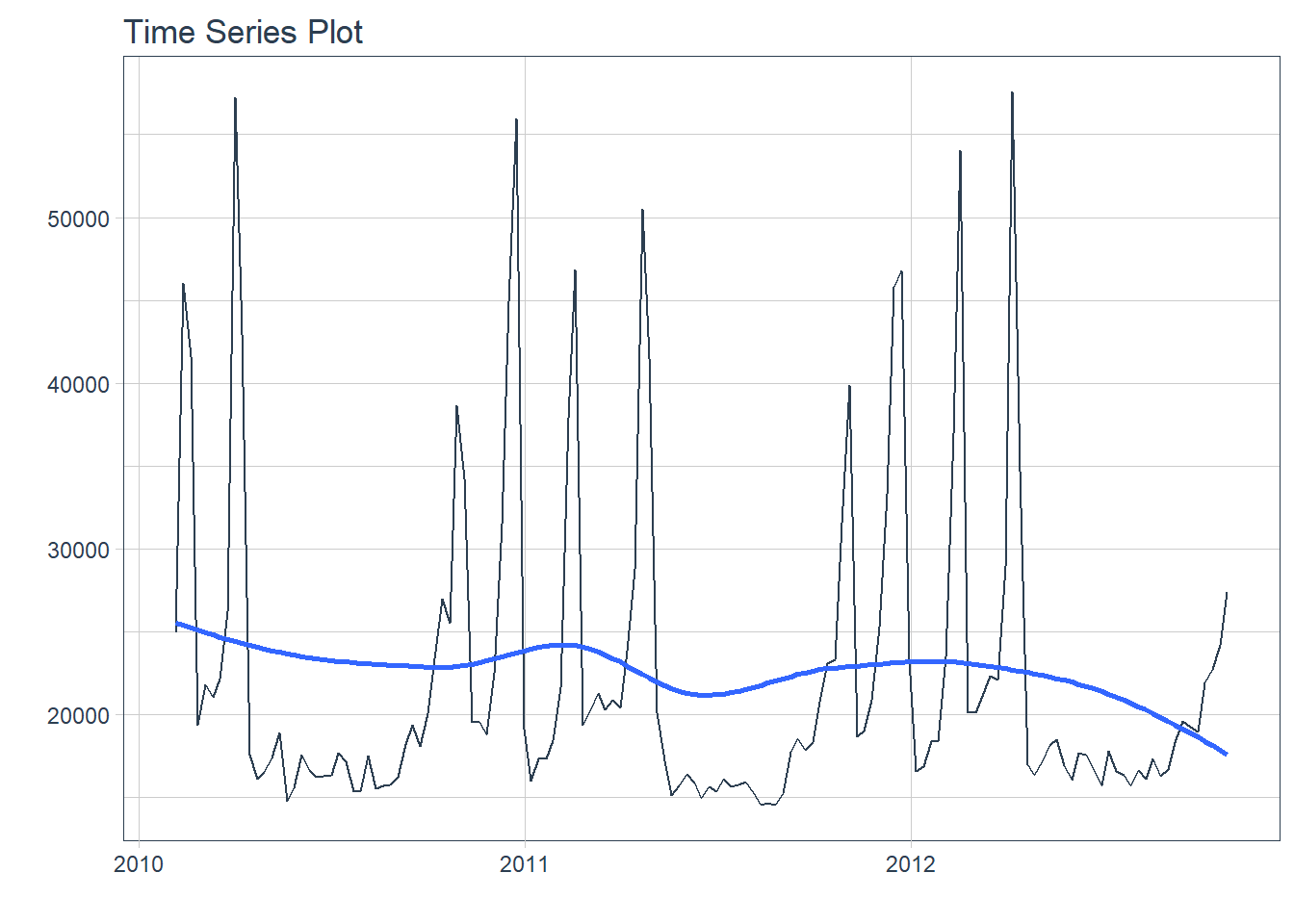
Figure 5.7: Vendas semanais do Departamento 1 da Loja na Walmart
Observamos alguns picos de vendas semanais que devem estar correlacionados a períodos de feriado. As vendas devem estar relacionadas ainda com a temperatura média e o preço do combustível naquela semana. Como temos acesso as covariadas Temperature e Fuel_Price podemos calcular não apenas o ACF, mas também a Função de Correlação-Cruzada com essas duas variáveis. Para tanto, vamos utilizar o parâmetro .ccf_vars na função plot_acf_diagnostics para incluir estas duas variáveis na análise.
walmart_sales_weekly %>%
group_by(id) %>%
select(id, Date, Weekly_Sales, Temperature, Fuel_Price) %>%
plot_acf_diagnostics(Date, Weekly_Sales, # Calcular ACF & PACF
.ccf_vars = c(Temperature, Fuel_Price), # CCF
.lags = "3 months",
.interactive = FALSE)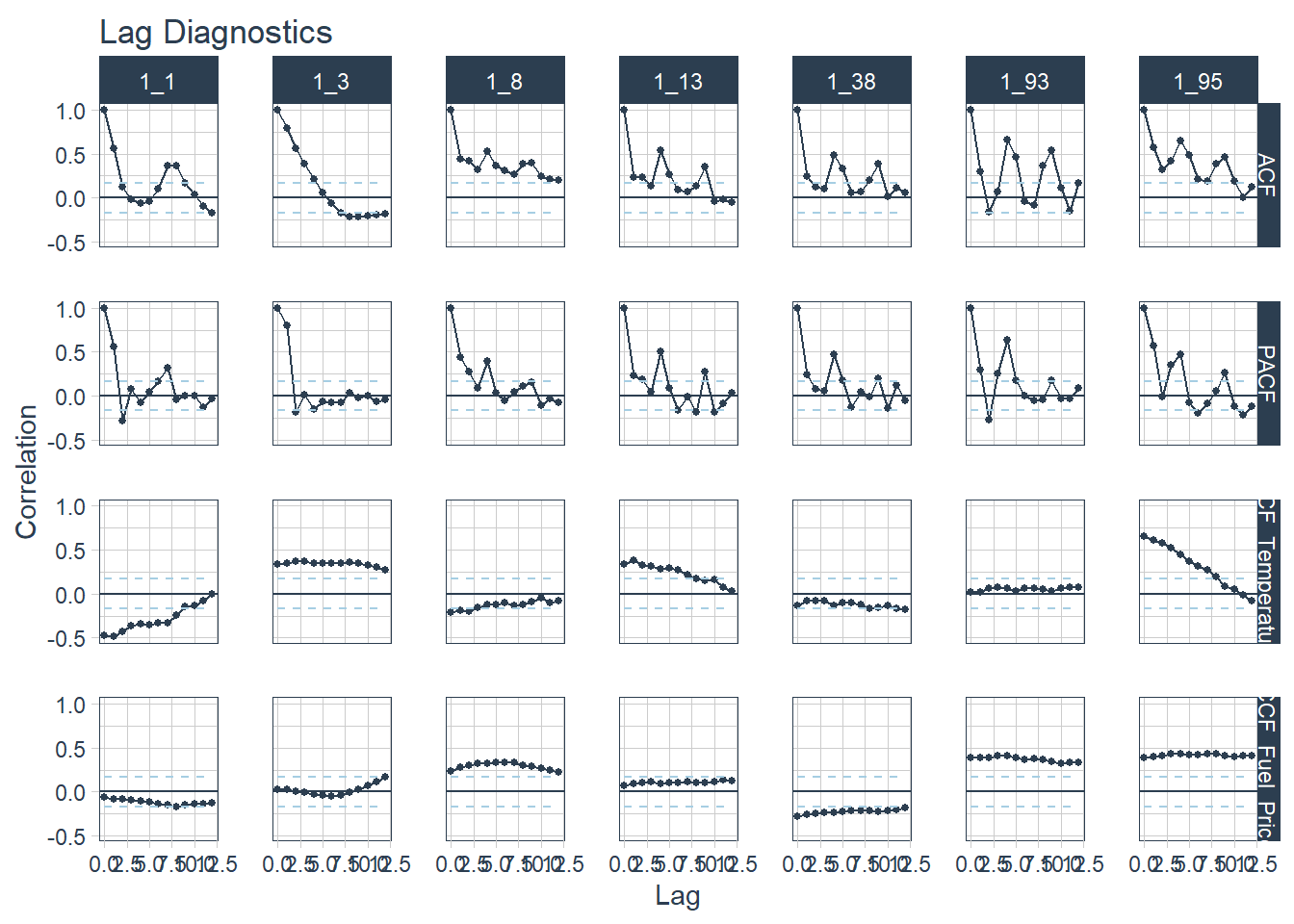
Figure 5.8: Correlação Cruzada de Vendas Semanais com Temperatura e Preço de Combustível
A função exibe o ACF e PACF de cada um dos departamentos de cada loja Walmart, além de calcular a correlação cruzada com temperatura e preço de combustíveis.
Uma análise da figura 5.8 sugere algumas relações curiosas, como a relação entre os valores de vendas semanais e valores passados de temperatura. A relação com temperatura pode ser diferente a depender da localização geográfica da loja, uma vez que em estados frios, baixas temperaturas associadas ao período de inverno podem desestimular a ida de clientes às lojas físicas, enquanto que em estados quentes, esse padrão não seria observado. Além disto, é possível que essa relação entre vendas e temperatura esteja sendo intermediada pelo padrão sazonal de vendas mais fortes no fim do ano.
É importante destacar que o padrão da correlação cruzada é afetado pela estrutura das duas séries e a tendência que cada uma tem. É preferível sempre remover a tendência das séries ou levar em consideração a estrutura do ARIMA univariado da variável \(x\) antes de aplicar um gráfico de CCF.