Capítulo 3 Características de Séries Temporais
Séries temporais se referem a dados observados em diferentes pontos no tempo. O uso de métodos estatísticos convencionais como o de regressão linear dependem e suposições de que as observações são independentes entre si, uma hipótese que não faz sentido quando se trabalha com observações no tempo: cada observação está correlacionada com as observações mais próximas no tempo. Assim, um choque no valor da ação que ocorre ontem tem efeitos no preço da ação hoje.
Na economia observamos a taxa semanal de juros, o preço de fechamento das ações, o índice de preço mensal, as vendas anuais, e por ai vai. Em meteorologia, observamos as temperaturas médias diárias, a precipitação anual, índices de seca e outros. Na agricultura temos o registro anual da colheita e da produção de leite, erosão do solo e valor das exportações. A lista de áreas em que séries temporais podem ser estudadas não tem fim.
O objetivo da análise de séries temporais são de: (1) entender ou modelar os mecanismos que produzem a série observada e (2) prever valores futuros de uma série com base na história da série, e quando possível, com relação a outras séries ou fatores.
3.1 Objeto ts
Uma série temporal pode ser representada como uma lista de números em sequência, onde cada número é uma informação sobre um período específico de tempo. No R, essas informações podem ser registradas como objetos ts.
A tabela 3.1 mostra um exemplo de dados anuais para o período entre 2012 e 2016.
| Ano | Observações |
|---|---|
| 2012 | 123 |
| 2013 | 39 |
| 2014 | 78 |
| 2015 | 52 |
| 2016 | 110 |
Podemos transformar as informações acima em um objeto ts utilizando a função ts():
y <- ts(c(123,39,78,52,110), start = 2012)
y## Time Series:
## Start = 2012
## End = 2016
## Frequency = 1
## [1] 123 39 78 52 110Se seus dados são anuais, com uma observação por ano, você precisa apenas fornecer o ano inicio (ou o ano final).
Para observações que são mais frequentes que uma vez ao ano, é preciso fornecer um argumento de frequência (frequency). Por exemplo, se seus dados são mensais, então ele pode ser convertido para um objeto ts da seguinte maneira:
dados_mensais <- c(10, 30, 50, 70, 90)
y <- ts(dados_mensais, start = 2015, frequency = 12)
y## Jan Feb Mar Apr May
## 2015 10 30 50 70 90Dados também podem ser observados como um objetivo do tipo data.frame. Neste caso, existe uma coluna de dados com as observações e outra coluna no formato de dados.
3.1.1 Frequências de uma série temporal
A frequência é o número de observações antes que o padrão sazonal se repita. Quando usamos a função ts no R, podemos utilizar as seguintes frequências:
| Dados | Frequência |
|---|---|
| Anual | 1 |
| Trimestral | 4 |
| Mensal | 12 |
| Semanal | 52 |
Em relação ao padrão semanal, na verdade temos \(365.25/7 = 52.18\) semanas em média em um ano, e não 52 semanas. Contudo, a maioria das funções que utilizam a função ts exigem que a frequency seja fornecida como um número inteiro.
Se a frequência de observações é maior do que uma vez por semana, existem algumas formas de lidar com a situação. Por exemplo, dados diários podem ter um padrão de sazonalidade semanal (frequency = 7) ou uma sazonalidade anual (frequency = 365.25). De modo similar, dados que são observados por minuto, podem ter um padrão sazonal a cada hora (frequency = 60), uma sazonalidade diária (frequency = 1440, ou \(24 \times 60\)), uma sazonalidade semanal (frequency = 10080, ou \(24 \times 60 \times 7\)) e anual (frequency = 525960, ou \(24 \times 60 \times 365.25\)).
Para utilizar um objeto ts nestes casos, é preciso decidir que desses padrões sazonais é mais importante. Contudo, o R permite lidar com dados com múltiplas sazonalidades utilizando técnicas mais avançadas.
3.2 Gráficos de Séries Temporais
Para séries temporais, o gráfico apropriado mostra as observações no tempo, com observações consecutivas sendo unidas por uma linha reta. A figura 3.1 mostra um exemplo de um gráfico de séries temporais.
library(fpp)
library(tidyverse)
autoplot(ausair) +
ggtitle("Total de Passageiros aéreos registrados na Australia, 1970-2009") +
xlab("Ano") +
ylab("Milhões")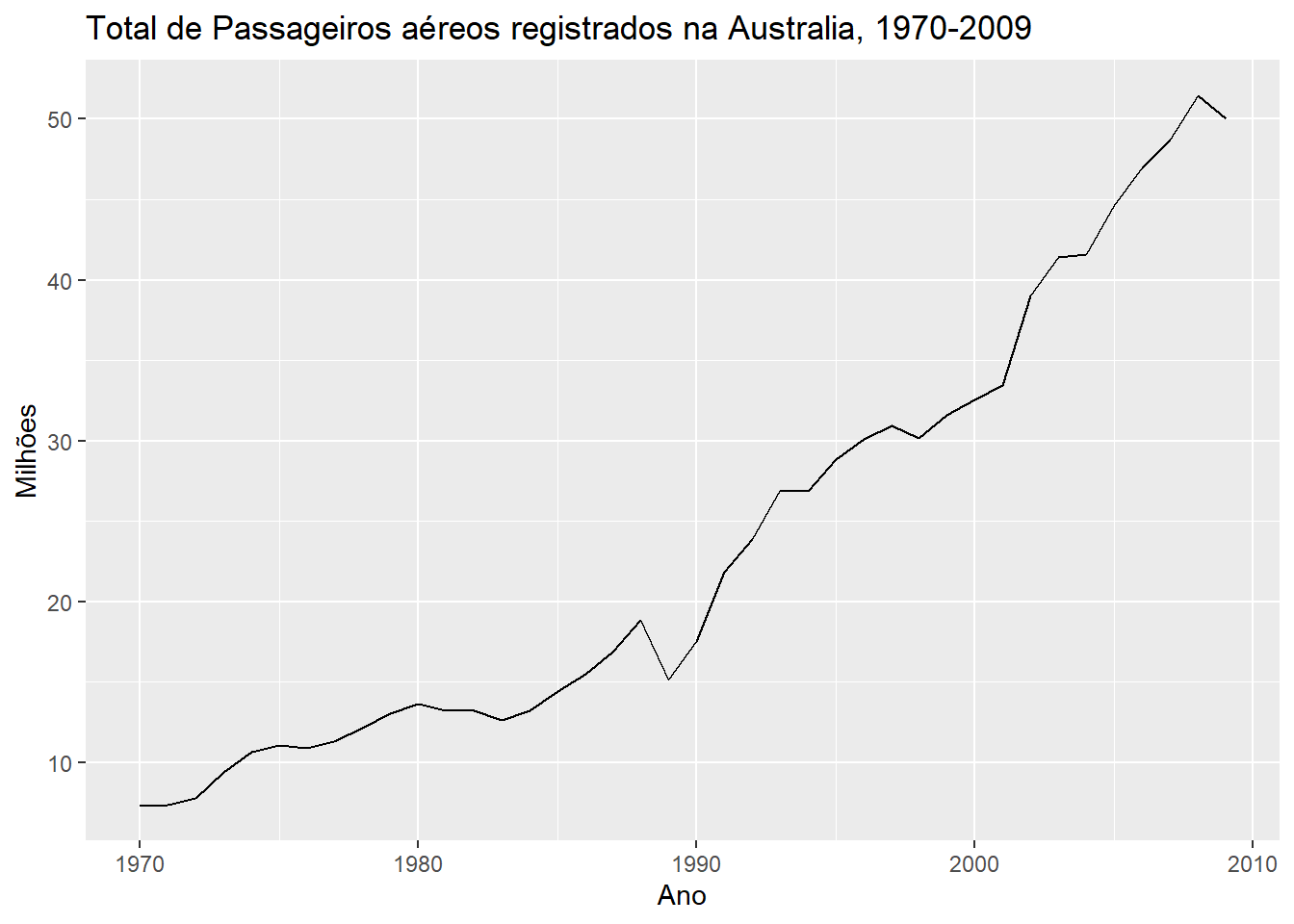
Figure 3.1: Total de passageiros semanais na Compainha Áerea Ansett
Os dados fazem parte do pacote fpp, que acompanha o livro Forecasting: Principles and Practice. Com a função autoplot(), produzimos gráficos no tempo a partir de objetos ts.
3.2.1 Convertendo tk para data.frame
Objetos ts podem não ser tão conveniente de trabalhar quanto objetos data.frame ou tibble. Quando trabalhamos com estes formatos, as informações de data e horário ficam em uma coluna específica.
O pacote timetk possui uma série de funções convenientes para converter objetos ts para outros formatos:
tk_tbl: converte o objetotspara um objetotibble(objeto equivalente a um dataframe).tk_tsfaz o caminho inverso.
Abaixo convertemos ausair utilizando a função tk_tbl().
library(timetk)
dados_passageiros <- ausair %>%
# converte ts em tibble
tk_tbl()
dados_passageiros %>% tail() %>%
knitr::kable()| index | value |
|---|---|
| 2004 | 41.59655 |
| 2005 | 44.65732 |
| 2006 | 46.95177 |
| 2007 | 48.72884 |
| 2008 | 51.48843 |
| 2009 | 50.02697 |
O mesmo resultado de tk_tbl() pode ser obtido com o código: dados_passageiros <- data.frame(data = time(ausair), passageiros = matrix(ausair))
Com dados_passageiros no formato data.frame é possível produzir um gráfico de séries temporais utilizando o pacote timetk e sua função plot_time_series(). Para tanto, informamos a coluna de data e de variável dependente (figura 3.2).
library(timetk)
dados_passageiros %>%
plot_time_series(.date_var = index, # variável de data
.value = value, # variável dependente
# title, y_lab e x_lab são opções de customização
.title = "Total anual de passageiros aéreos na Australia, 1970-2009",
.y_lab = "Em milhões",
.x_lab = "Ano")Figure 3.2: Total anual de passageiros na Australia
Independemente da forma como o gráfico é produzido, ele revela algumas características interessantes:
Em 1989 houve uma redução abrupta no número de passageiro transportados.
O mesmo ocorre me 2008/2009.
Existe uma tendência geral de aumento no número de passageiros.
Como os dados são anuais, não podemos observar padrões sazonais dentro de um ano.
Para realizar previsão dessa série, todas essas características precisam ser levadas em conta.
Uma alternativa à função plot_time_series() para produzir gráficos de séries temporais,
é o pacote ggplot2. Por exemplo, é possível gerar o mesmo gráfico acima com o código ggplot(aes(x = index, y = value)) + geom_line() após carregar o pacote com library(ggplot2).
3.3 Padrões das Séries Temporais
Séries temporais podem ser descritas por seu padrão de comportamento. Usamos palavras como tendência, sazonalidade e padrão cíclico para descrever esses padrões. Modelos de previsão tentam utilizar estes padrões para realizar previsões.
3.3.1 Série Sem Padrão
Na figura 3.3 vemos a média de precipitação na cidade americana de Los Angelos durante o período de 1878 a 1992. Estes dados estão no pacote TSA, que acompanha o livro Cryer and Chan (2008).
library(TSA)
data(larain)
larain_tbl <- larain %>%
tk_tbl() %>%
rename(chuva_anual = value,
data = index)
larain_tbl %>%
plot_time_series(.date_var = data,
.value = chuva_anual,
.title = "Chuva Anual em Los Angeles, 1878 - 1992",
.x_lab = "",
.y_lab = "Precipitação em polegadas")Figure 3.3: Padrão de Chuvas em Los Angeles
É possível perceber uma variação no volume de chuvas ao longo dos anos – alguns anos com um volume de chuva mais alto, outros mais baixo.
Estamos interessados se os valores da chuva estão relacionados entre si. Será que ao conhecer o comportamento da chuva em um conjunto de anos podemos prever o que ocorrerá em anos consecutivos?
Para responder esta questão, podemos criar uma variável relativa a chuva do ano anterior e compara-la com a chuva no ano corrente utilizando a função lag(). Na figura 3.4 exibimos as duas informações lado a lado com um gráfico de dispersão.
larain_tbl <- larain_tbl %>%
mutate(chuva_ano_anterior = lag(chuva_anual))
larain_tbl %>%
ggplot(aes(x = chuva_anual, y = chuva_ano_anterior)) +
geom_point() +
geom_smooth() +
labs(x = "Chuva anual",
y = "Volume de chuva do ano anterior",
title = "Volume de Chuva em Los Angeles, 1876 - 1992",
subtitle = "Relação entre a Chuva Anual e o Volume de Chuva no Ano Anterior")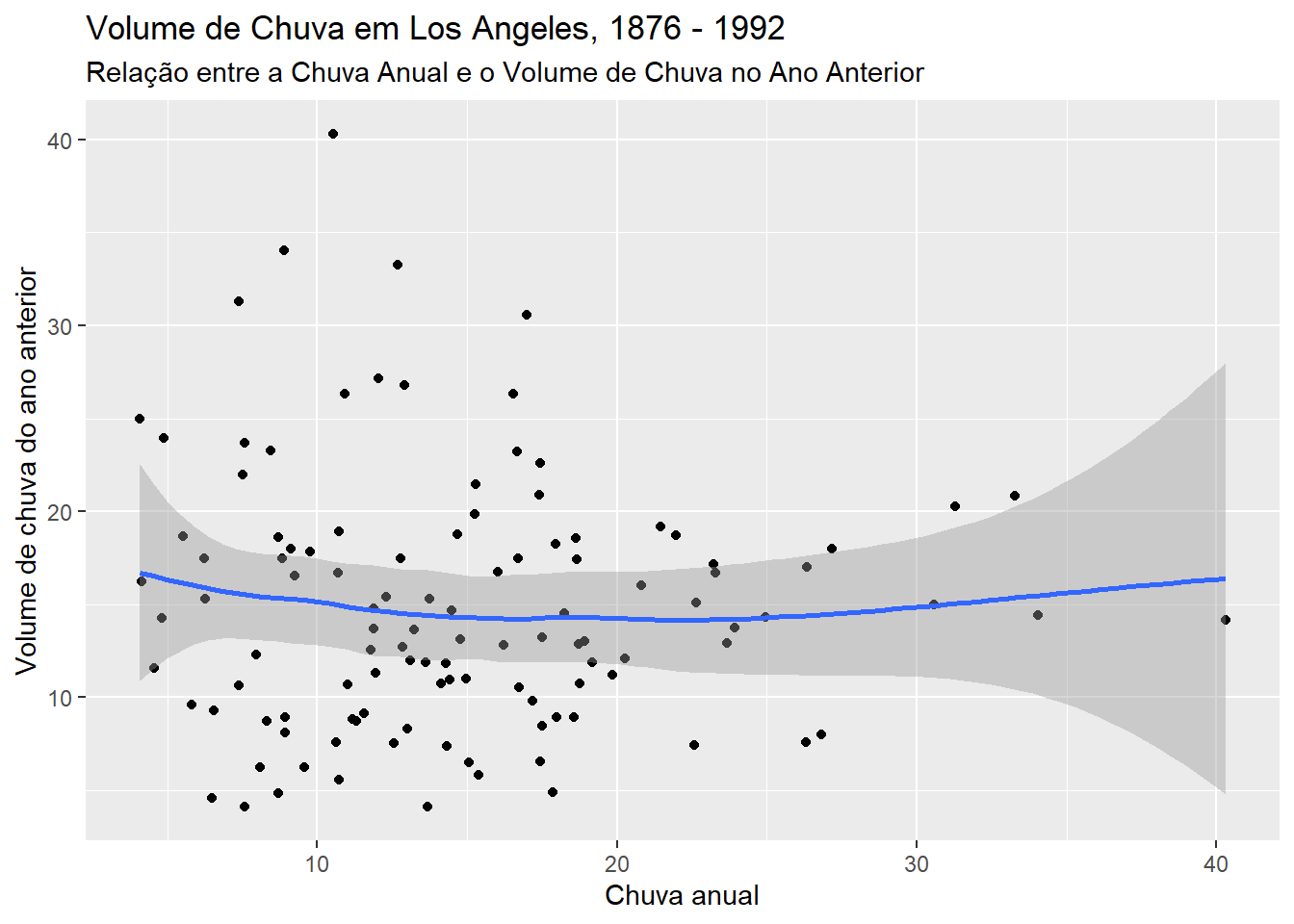
Figure 3.4: Relação entre chuva atual e o volume de chuva do ano anterior
É possível observar que é perfeitamente possível que um ano com um elevado volume de chuvas seja seguido por um ano com baixo volume, e vice-versa. Assim, o volume de chuva que ocorre em um ano não explica muito bem o comportamento da chuva nos anos seguintes.
Essa série não parece ter nenhum tipo de tendência, que indicaria que o volume de chuva está aumentando ou diminuindo ao longo do tempo. Não parece existir correlação entre a chuva de um ano e do ano anterior, de modo que podemos ter um ano com um volume muito alto de chuva e no ano seguinte, um volume baixo. De um ponto de vista de modelagem e de previsão, está não é uma série muito interessante.
3.3.2 Uma Série com Padrão
A figura 3.5 mostra uma série de total anual de coelhos canadenses para o périodo entre 1905-1934.
data(hare)
hare_df <- hare %>%
tk_tbl() %>%
rename(data = index,
ambudancia_coelhos = value)
hare_df %>%
plot_time_series(.date_var = data,
.value = ambudancia_coelhos,
.smooth = FALSE,
.x_lab = "Ano",
.y_lab = "Ambundância de Coelhos",
.title = "Ambundância de Coelhos Canadenses, 1905-1934")Figure 3.5: Ambundância de Coelhos Canadenses
Diferentemente da série de chuva em Los Angeles, as observações de um ano estão correlacionadas de maneira muito próxima com aquelas observadas no ano anterior. Um número grande em um ano é seguido de um número semelhante no ano seguinte.
Na figura ?? é possível observar com mais clareza como existe uma relação entre a ambudância de coelhos de anos consecutivos.
hare_df %>%
mutate(ambudancia_ano_anterior = lag(ambudancia_coelhos)) %>%
ggplot(aes(x = ambudancia_coelhos, y = ambudancia_ano_anterior)) +
geom_point() +
geom_smooth()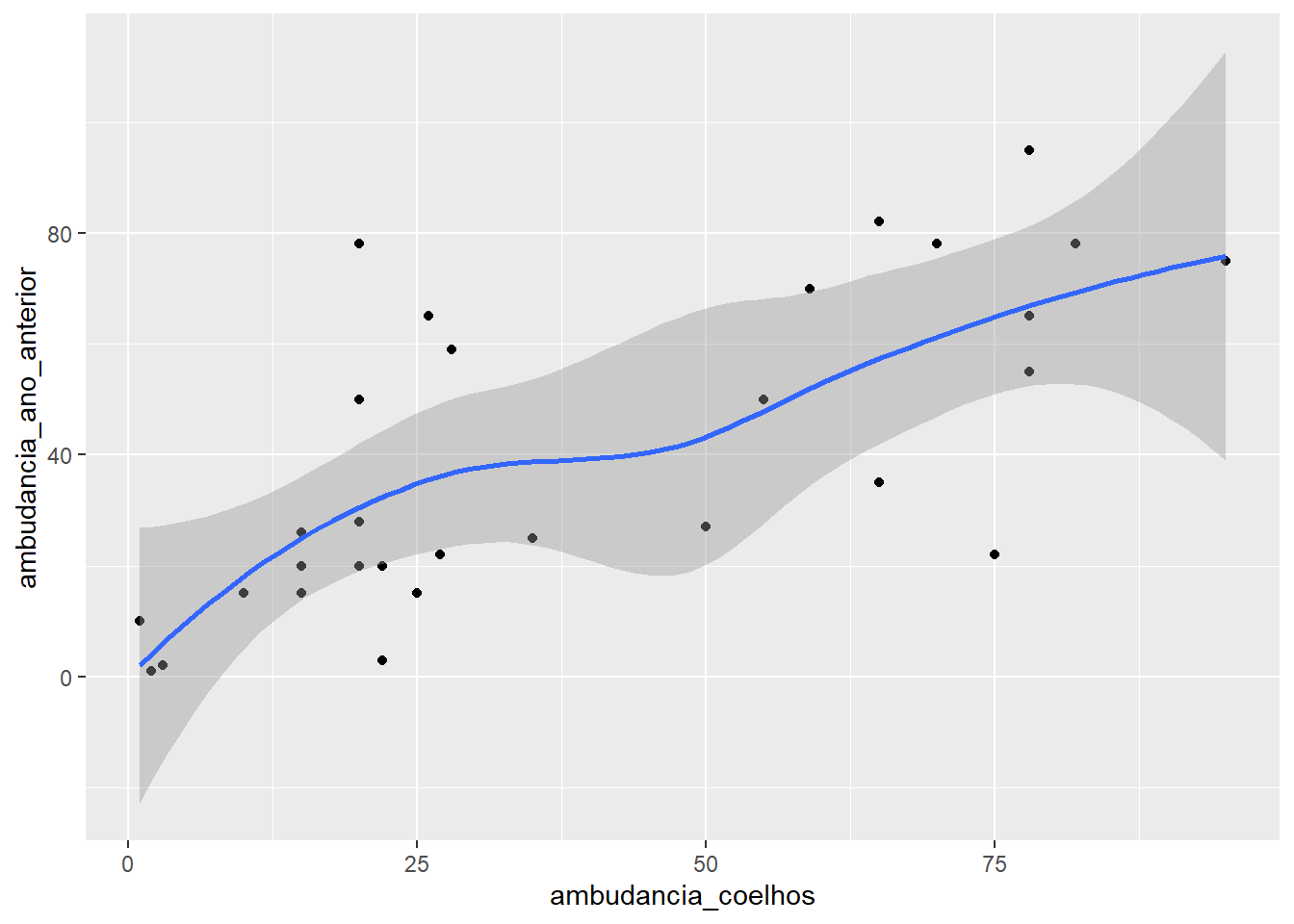
Figure 3.6: Correlação entre ambundância de coelhos de anos consecutivos
3.3.3 Sazonalidade
Um padrão sazonal ocorre quando uma série é afetada por fatores sazonais como o tempo do ano ou o dia da semana. Sazonalidade é sempre de uma frequência conhecida e fixa.
A figura 3.7 mostra uma série temporal de temperatura mensais registradas para uma cidade no estado americano do Iowa.
data(tempdub)
tempdub %>%
tk_tbl() %>%
rename(data = index,
temperatura = value) %>%
plot_time_series(.date_var = data,
.value = temperatura,
.x_lab = "Ano",
.y_lab = "Temperatura",
.title = "Temperatura Média Mensal no Estado do Iowa, 1964-1976")Figure 3.7: Temperatura média anual em Iowa
Nela observamos uma movimento sazonal muito regular. Sazonalidade para valores mensais ocorre quando observações que são separadas por 12 meses estão relacionados de alguma maneira. Assim, as temperaturas em janeiro de 1910 estão relacionadas com as temperaturas de janeiro de 1911, 1912 e assim por diante. Todos os meses de janeiro e fevereiro são muito frios e são similares em valores de temperatura. O que não quer dizer que todos os meses de janeiro terão a mesma temperatura, ou os meses de junho terão sempre a mesma temperatura média.
Se desejarmos prever os valores futuros de temperatura em Iowa, precisamos de um modelo capture estas similaridades entre temperaturas dos mesmos meses.
Abaixo vemos um outro exemplo de série sazonal (figura 3.8). Ela exibe uma série de vendas de drogas contra diabetes nos EUA. A série possui um comportamento sazonal bastante marcante.
a10_df <- a10 %>%
tk_tbl() %>%
rename(data = index,
vendas_drogas = value)
a10_df %>%
plot_time_series(data, vendas_drogas,
.x_lab = "Ano",
.y_lab = "Milhões de US$",
.title = "Vendas de Drogas Anti-diabéticos")Figure 3.8: Vendas de Medicamento contra diabetes
Como temos uma série mensal de vendas de drogas ao longo dos anos, podemos verificar o comportamento a sazonalidade dentro dos anos, trimestres e meses. O pacote timetk oferece uma a função plot_seasonal_diagnostics(), que produz uma série de sub-séries sazonais. A figura @ref(fig:seasonal_timetk) a saída desta função.
library(timetk)
a10_df %>%
plot_seasonal_diagnostics(data, vendas_drogas, .interactive = F)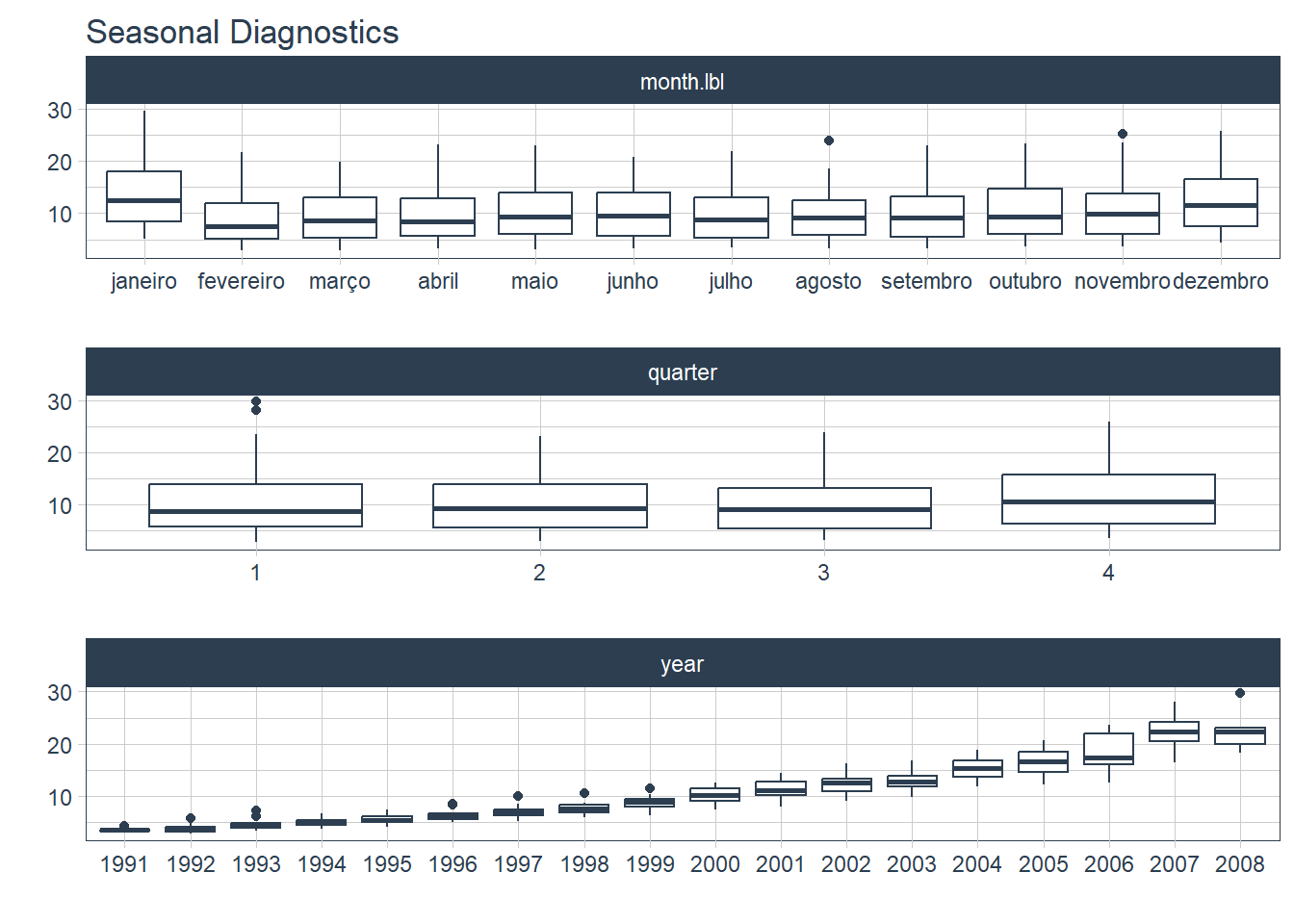
(#fig:seasonal_timetk)Gráfico sazonal das vendas mensais de medicamentos contra diabetes
A figura nos permite observar o padrão sazonal com mais clareza, e é especialmente útil para entender o padrão interno dentro de um ano, assim como encontrar anos com mudanças de padrão. Especificamente observamos um aumento significativo da venda de drogas no início do ano.
3.3.4 Tendência
A série de vendas de drogas também exibe um padrão de tendência. Uma tendência ocorre quando existe um aumento (ou redução) de longo prazo nos dados. A tendência não precisa ser linear, e muitas vezes pode apresentar mudanças de direção, que ocorrem quando uma tendência de aumento se converte em uma tendência de queda.
A figura 3.9 mostra outra série com padrão forte de tendência crescente.
cafe %>%
tk_tbl() %>%
plot_time_series(index, value,
.title = "Gastos Trimestrais com consumo fora do domicílio, Australia",
.x_lab = "Ano",
.y_lab = "Milhões")Figure 3.9: Gastos com consumo fora do domicílio na Australia
Os gastos dos australianos com consumo fora do domicílio (cafés e restaurantes) tem uma tendência crescente durante todo o período. Ela também exibe um comportamento sazonal dentro de um mesmo ano.
3.3.5 Padrão Cíclico
Um comportamento cíclico surge quando os dados exibem um padrão de altas e quedas que lembra a sazonalidade, mas ao contrário desta, o ciclo não possui frequência fixa. Muitos confundem o comportamento sazonal, mas eles são bem diferentes. Se a flutuação não tem frequência fixa, temos um ciclo; se a frequência não se altera e está associada com algum aspecto do calendario, então o padrão é sazonal.
Em geral, o tamanho médio dos ciclos é maior que o comprimento de um padrão sazonal, e a magnitude dos ciclos tende a variar mais do que a magnitude do padrão sazonal. Além disto, as flutuações dos ciclos são o resultado, quase sempre, de condições econômicas, e estão relacionadas ao ciclo de negócios. A duração dessas flutuações tendem a ser de no mínimo 2 anos.
A figura 3.10 mostra informações sobre a fabricação de equipamentos elétricos na zona do Euro.
elecequip %>%
tk_tbl() %>%
plot_time_series(index, value,
.title = "Equipamentos Elétricos Produzidos na Área do Euro",
.x_lab = "Ano",
.y_lab = "Índice 2005 = 100")Figure 3.10: Equipamentos elétricos produzidos na zona do Euro
É possível observar um padrão sazonal dentro de cada ano, mas também um forte comportamento cíclico com um período de cerca 5 anos ou mais.
3.4 Decomposição
Vimos que uma série de tempo possui três padrões básicos: tendência, sazonalidade e ciclo. Uma série de métodos são utilizados para separar estes padrões em componentes individuais. Geralmente, os componentes de ciclo e tendência são exibidos em conjunto (e chamados apenas de tendência), de modo que uma série temporal pode ser vista como composta de três partes: um componente de ciclo-tendência, um componente de sazonalidade e o resto.
Algumas séries, sobretudo de alta frequência (minutos, dias, semanas), podem exibir múltiplos componentes de sazonalidade, correspondentes a diferentes períodos sazonais.
3.4.1 Decomposição STL
A Decomposição de Tendência e Sazonalidade usando Loess (STL em inglês) é um método versáil e robusto para decomposição dos componentes de séries temporais. Uma das suas vantagens é a possibilidade de decompor qualquer tipo de sazonalidade, e não apenas mensal e trimestral como outros métodos.
A decomposição STL é implementada no R com a função stat::stl(). O pacote timetk fornece uma versão conveniente desta função com plot_stl_diagnostics(). A função plot_stl_diagnostics() tem dois parâmetros principais:
.frequency: parâmetro que permite ajustar o componente sazonal. Para a série acima, os dados são mensais, de modo que temos uma frequência de 12..trend: parâmetro que ajusta a janela de tendência. Uma inspeção parece indicar que os ciclos duram cerca de cinco anos em média.
O valor padrão destes dois parâmetros é "auto, que permite que a função calcule automaticamente o período de sazonalidade e a janela de tendência. Vamos aplicar esta função aos dados de equipamentos elétricos produzidos na zona do Euro (3.10). A figura 3.11 mostra o resultado desta decomposição STL.
elecequip_df <- elecequip %>%
tk_tbl() %>%
mutate(index = as.Date(index))
elecequip_df %>%
plot_stl_diagnostics(index, value,
.title = "Decomposição STL da Série de Produção de Equipamentos Elétricos",.facet_scales = "free_y")Figure 3.11: Decomposição STL da Série de Produção de Equipamentos Elétricos
Na figura vemos cinco séries: (1) a série observada; (2) o componente sazonal extraído; (3) o ciclo-tendência; (4) o resto, que representa a série filtrada da sua tendência e sazonalidade; e a série ajustada sazonalmente.